Can Male Advantages in Intelligence Explain Why Geniuses are Disproportionately Male?

No.

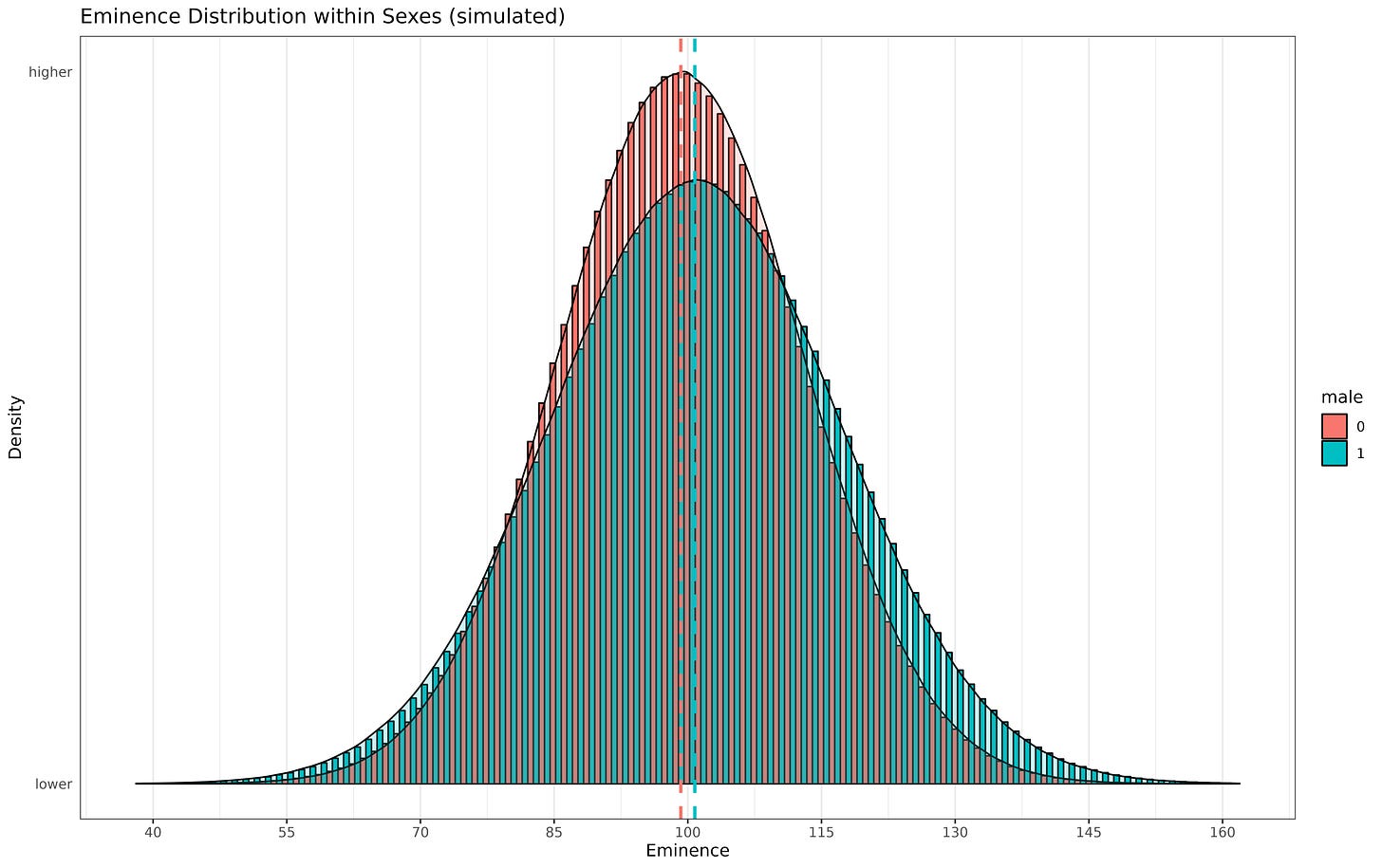
The best estimate of the male advantage in intelligence is roughly 3 points and men also have slightly greater variance in intelligence (SD ratio = 1.18, extrapolating from d = 0.2 and a VR of 1.4). These are controversial (if not outright fringe) beliefs, but for now they will serve as a steelman to knock down.

A distribution of male and female IQs with those parameters looks like this:

d = 0.21, VR = 1.4, which translates to a SD ratio of 1.18

To determine whether the sex difference in intelligence is causing men to be more likely to be geniuses, the IQ of the average genius, as measured by eminence and achievement, must be determined. Roe estimated that the average IQ of an eminent scientist was about 152 based on a sample of 64 scientists, many of which were nobelists. At first I thought this was an overestimate, but then I thought about for a bit and it started to make sense. The best scientists with the lowest recorded IQs, as far as I know, are EO Wilson who scored 123, and William Shockley who scored 119, 125, and 129 on three separate attempts. If it is assumed that the distribution of the IQs of eminent scientists has a mean of 150 and standard deviation of 10-15, the lowest scorers would be expected to score as low as Shockley and Wilson, making the estimate much more credible.

It’s also probably the case that great scientists have higher IQs than their counterparts in social scientists, musicians, or writers. For what it’s worth, the average of the eminent social scientists that I have estimated the IQs of is roughly 142, based on the following figures:

• Richard Lynn: 131

• Charles Murray: 136

• Gwern: 136

• Scott Alexander: 138

• Jordan Peterson: 138

• Arthur Jensen: 145

• Curtis Yarvin: 154

• Steven Pinker: 159

This could be biased by the fact that extremely intelligent people are more likely to have public IQ scores or test scores. However, the figure is not that different from the average of the eminent scientists Roe sampled, and three of these figures were obtained through private communications (Yarvin, Pinker, and Lynn), two of which are at the top of the list. The figures are unlikely to be biased due to poor estimation, as every single one was estimated using either a standardized test or IQ test.

Even if it isn’t clear what the IQ of the average genius is, it would probably be safe to conclude that the average genius has an IQ of about 145, though this figure could reasonably lie anywhere between 135 and 155.

Another figure that must be quantified to do the analysis is the proportions of geniuses who are men. Within Murray’s Human Accomplishment, he determined that about 97.8% of significant figures were men.

from here

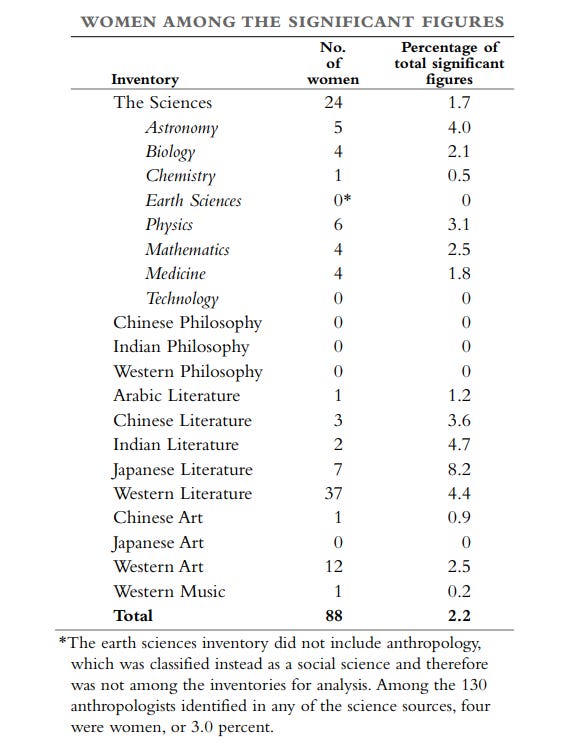
This could potentially be biased by the fact that women are less likely to be noticed in lists of the most significant people of the world. Murray doesn’t think this is the case for several reasons:

1. Not only are women less likely to be significant figures, they tend to be less eminent within the sample of significant figures (see page 268).

2. For every notable female scientist who was not included on the list of significant figures, there are somewhere between 60-120 men with biographies as long or distinguished as theirs in the Dictionary of Scientific Biographies who were not included on the list either (see pages 268-273).

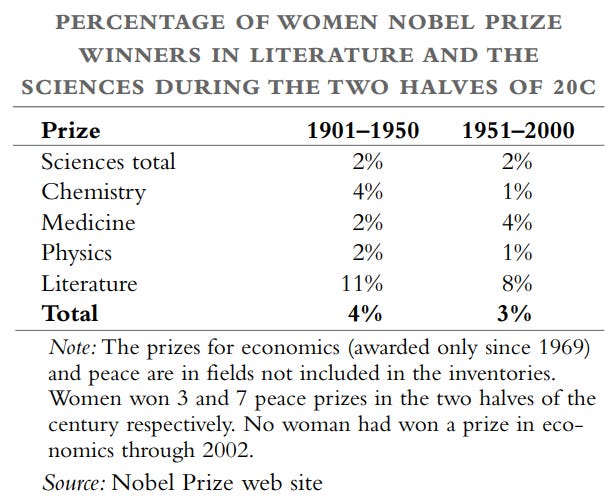
3. The percentage of women who won nobel prizes in both halves of the 20th Century was fairly constant at 3-4%.

I’m willling to go farther than Murray - that men are about 99-99.5% of geniuses and not 97.8%. Demographic outliers like Marie Curie or Thomas Sowell are not unfairly ignored, instead they tend to draw attention because they are unique. For now, I’ll stick with the estimate of 98% for the sake of the face.

II.

Using the simulated data I created for the first figure, people can be excluded until a mean of 145 is achieved. Within the simulated distribution of geniuses, 87% of them were men (n = 2313).

d = 0.75 within the high ability sample (95% CI: [0.63, 0.87])

Converting these figures to odds ratios, the effect of being male on the odds being in the distribution of IQ of geniuses is 6.53. In contrast, the effect of being male on the odds of becoming an actual genius is 50. So while sex differences in IQ do play a role in male overrepresentation, they only explain a fraction of the difference.

Increasing the estimated mean of geniuses to 155 (which is unrealistic) increases the expected percentage of geniuses who are men to 95% (n = 1062). This might look close to the observed number, but in terms of odds ratios, the effect of being male on being within the (exaggerated) IQ distribution of geniuses is 20, which is still far from the observed odds ratio of 50 in real life geniuses.

III.

If eminence is roughly normally distributed, the male advantage in eminence is roughly what you would expect from the correlation between IQ and eminence (let’s assume it’s r = .5), and GMV in eminence is the same as the observed GMV in intelligence, the sex ratio at each cutoff of eminence can be computed.

d = 0.105, VR = 1.4 in favour of men in “latent eminence” is assumed

The estimated percentage of men (97-99%) within geniuses (>4-5 SD) is almost exactly the observed number of geniuses that are observed in real life (98-99%). So, the fact that there is more male geniuses is probably because they psychologically vary more in general, not because they vary more in intelligence.