Contra Dynomight: controlling for variables works

Dynomight has made the case that controlling for variables does not usually work.

I.

Controlling for variables in statistics means calculating the relationship between two variables that would be expected when holding another set of variables constant. For example, in a study on honesty and intelligence, I found that honest people tended to be more intelligent. Theoretically, this could be confounded by race or the fact that people born into high status homes are more intelligent and honest. To deal with this problem, I used multiple linear regression, a statistical technique which involves using linear algebra to determine the independent linear effect of several variables on a dependent variable.

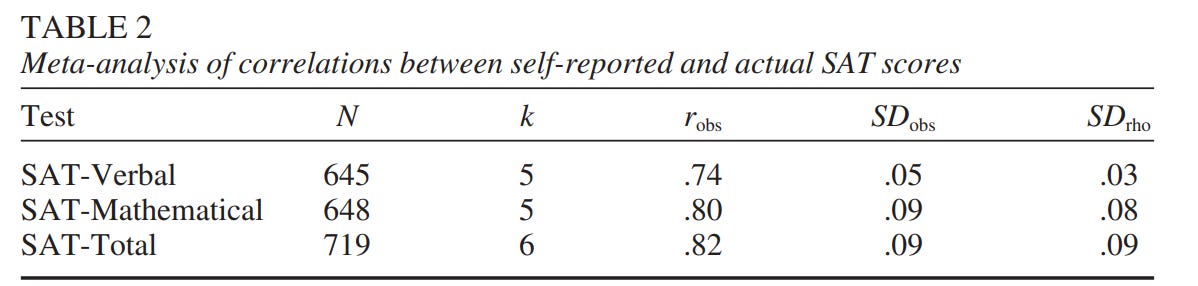
In the following table, the independent variables are a composite of parent education/wealth/income (SES), ASVAB factor score (IQ), and race, which are all predicting a composite of parent reported, self reported, and interviewer reported honesty.

from here

Before controlling for IQ (model 3), Black people, Hispanic people, and people born in low status households are more dishonest, but these relationships disappear or attenuate after controlling for IQ (model 4). Why this is the case is unclear: I discuss several theories in the paper, but I think the most likely one is that intelligent and competent people have less to gain by lying.

II.

The first argument Dynomight raises against controlling for variables is an intuitive argument — that multiple linear regression cannot intuitively parse out causality.

To start, just use your intuition. Does it seem like you can uncover causal relationships by doing little regressions?

Think about the previous dataset. There are many possible relationships between weight, alcohol, and calories. Maybe being heavier makes people drink more. Maybe drinking makes people eat more. Maybe alcohol and food directly do nothing, but they’re correlated with exercise, which is actually what determined how fat people are. Maybe the true relationship is nonlinear, and all the variables influence each other in feedback loops. Any of these relationships could produce the previous data.

You could use this argument against any statistical or machine learning method that is not a black box; this issue is not specific to regression. Panel data results can be confounded by reverse causality, zero order correlations can be biased by confounders. When quantitative evidence and intuition collides, usually intuitions are correct, but this is not always the case.

In the 1960s, the Coleman report was released, a study of achievement differences between 650,000 Black and White students on the national scale. They found many things that contradicted people’s intuitions: achievement differences between Blacks and Whites could not be blamed on the schools, but on what the students were bringing to them; that school funding didn’t really matter than much; and that there were massive differences between regions and races: the average black twelfth grade student in the rural South was achieving at the level of a seventh grade white student in the urban Northeast.

III.

The other issues he raises with using regression are similar in nature: they can be reduced to the observation that controlling for variables does not address the direction of causality:

Take a group of aliens that only vary in how much they drink and how fat they are. Nothing else matters: They don’t eat or exercise, they all have the same genes, etc. Now suppose drinking and weight are positively associated. There are three possible explanations:

First, maybe drinking makes them heavier. (Perhaps because alcohol has calories.) We can draw this as:

    ALCOHOL → WEIGHT.

Second, maybe being heavier causes them to drink more. (Perhaps because there’s a hormonal change in heavier people that makes alcohol taste better.) We can draw this as:

    ALCOHOL ← WEIGHT.

Third, maybe drinking and weight are in some kind of complex feedback loop. (Perhaps because both of the above things happen.) We can draw this as:

    ALCOHOL ↔ WEIGHT.

How do you use observational data to figure out which explanation is right?

The answer is easy: You don’t.

Again, this issue is not specific to regression. Regression examines the association between one variable and another that would be found if another set of variables was held constant; not whether one variables causes another. This is a broader problem with observational studies.

In practice, making ad hoc causal explanations from observed correlations in science can be done if the correlation is strong enough. Consider some of the strongest correlations in the ABCD dataset:

from here

In 14 of 17 cases there is an obvious causal relationship: biological maturation in children causes weight and height and reading ability causes school performance. Regression can help beat the dead cow, but in many cases it is unnecessary.

IV.

He later raises simple, but more relevant objections to the use of regression, including:

Missing causes. There might be important variables that are missing from the model. Sometimes these are things that you just failed to measure (like EXERCISE). Sometimes these are ethereal and unmeasurable (like PSYCHOLOGICAL COMMITMENT TO A HEALTHY LIFESTYLE).

That’s a fair point, though the magnitude of this issue varies on a case by case basis. If it is found that IQ tested in adolescence is associated with income even after controlling for race, parental SES, region, birth order, it would be rational to conclude that IQ causes income.

On the other hand, if the relationship between being thin as an adolescent and income as an adult survives controls for parental social status, it is still doubtful whether there is a causal relationship between the two variables.

Linearity. Fitting linear models assumes interactions are linear. Often there’s a feeble attempt to address this by testing what happens if you add interactions or quadratic terms. But there’s no guarantee that a quadratic model is sufficient either. And people often do weird things like compute a p-value for the quadratic term, observe that the p-value is large, and therefore conclude that the quadratic term isn’t needed. (That isn’t how p-values work.)

That’s a good one, though multiple regression models can still accept restricted cubic splines. A bit too esoteric for most, unfortunately.

Coding. Everything depends on how you code variables. Like, when people say they control for “education”, what they actually did is choose some finite set of categories, e.g. (highschol or less) / (some college) / (4-year degree or more). But you could break these things up differently, and when you do, the results often change.

Noisy controls. People might say they control for “diet”. But what they actually control for is “how much people claimed to eat on 5 days they were surveyed”. If they don’t remember, or they lie, or those days were unusual, what happens? Well, in the limit of pure noise, the regression will just ignore the control variables, equivalent to not controlling at all. In practice, the effect is usually somewhere in the middle, meaning that things are just partially controlled. It’s amazing how rare it is for papers to show any awareness of this issue.

The reliability of measures does affect the degree to which regression is effective. If there is a focus, dependent, and control variable, and the focus/control variables are not measured accurately, the type I error rate inflates.

Consider this: most measures in psychology are quite reliable.

• IQ: about .91, depends on test and length of retesting interval.

• IPIP-NEO neuroticism: .90

• IPIP-NEO extraversion: .89

• IPIP-NEO openness: .83

• IPIP-NEO agreeableness: .87

• IPIP-NEO conscientiousness: .90

• MMPI scales:

• Educational attainment (from an unreleased, recently accepted paper):

  

• Self-reported SAT scores and GPA:

Pooling all of the correlations together results in an average reliability of .81.

As the average effect size in psychology is about .19 (in normal literature, .16 when preregistered), the degree to which unreliability biases normal psychological research can be estimated using simulations.

Assume we have variables A, B, and C. A has a small causal effect (r = .2) on both B and C. All variables are measured inaccurately (rxx = .81). A regression is run where A and B are predicting C, and the desired result is that A is associated with C but not B.

The following statistics were estimated using n = 10k simulations: the standard false positive (type I) error rate (effect of B on C is p < .05), strong type I error rate (effect of B on C is p < .001), power (effect of A on C is p < .05), and the strong power (effect of A on C is p < .001) can be easily simulated under varying sample sizes.

It turns out that, in this model, the unreliability of the variables is not an issue. Standard type I errors start to become an issue as the sample sizes increase from 5000 to 20000, and egregious type 1 errors (false p < .001) practically never happen regardless of the sample size. In the following table:

n = simulated sample size

meantype1 = likelihood of finding a false positive that passes p < .05

meantype1strong = likelihood of finding a false positive that passes p < .001

meanpower = power of finding p < .05

meanpowerstrong = power of finding p < .001

Note that p-values are not the only way regression tables can be interpreted; the amount an association shrinks after controlling for a variable can also be observed. For example, if the correlation between B and C is .05, but the correlation after controlling for A is only .01, then the effect has shrunk by 80%. It turns out that in most cases, the effect shrinks by over 50%, and the variance of the shrinkage effect decreases massively with sample size.

Inadvertently, I also discovered that the shrinkage statistic is biased, where smaller samples give a larger than expected shrinkage effect.

Even though type 1 errors are easily committed in larger datasets, this is offset by the fact that shrinkage effects are more reliably observed in larger datasets.

The paper I cited earlier found roughly the same results: the estimated type I error rate they found in n = 30,000 | rxx = .80 | ES = .20 was 25%. For n = 20,000 | rxx = .81 | ES = .20 I found an expected type I error rate of 15%. For 50,000, I found 30%.

from here

V.

Dynomight also wrote that controlling for variables fails in practice several times. It would be overkill to go over his examples in detail, but I have a few comments:

• SAT vs GPA: He finds that a study which found that test scores were not that predictive after controlling for GPA, student demographics, and the graduation rate of their school. A fair example, but the issues with the analysis are a bit obvious: the students are being selected for test scores, and the graduation rate of the school is an indirect measurement of student quality.

• Apsartame: I lost interest in both articles he wrote on this topic quickly, because I found the first argument he made (aspartame is quickly converted into harmless amino acids) to be plausible enough. Besides that, I found his citation of the scientific consensus to be stupid, because if a topic is debated despite there being a scientific consensus, then that indicates that the consensus might be wrong because people bother to attack it. In his defense, that argument would seem credible to his audience. I also found his dismissal criteria for studies (obscure institutions and authors) to be silly.

• Diet soda and autism: a study found that diet soda exposure in fetuses and newborns and autism were linked after controlling for a set of variables. His argument (small sample size, confounders are irrelevant, and poorly measured) looked reasonable enough to me.

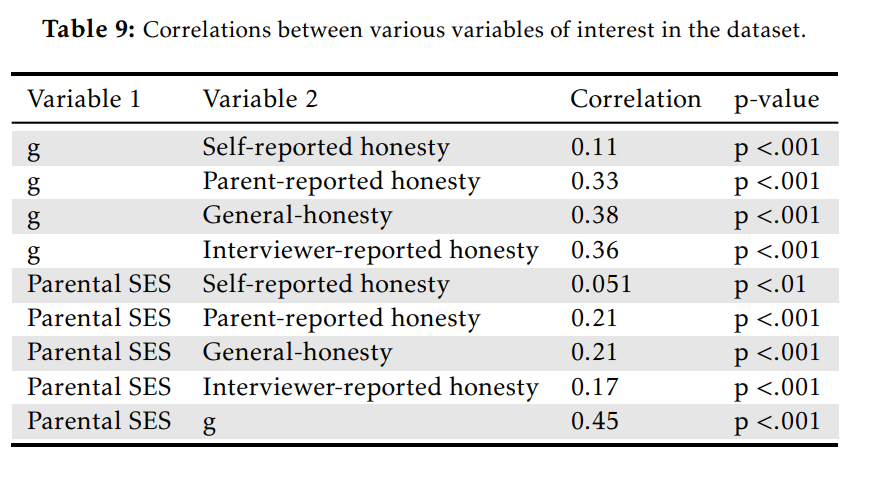
There are, admittedly, some cases where regression flunks. But there are many more situations where regression works just fine. Take the paper on honesty, intelligence, and race I mentioned earlier: both intelligence and parental SES correlate with a range of measures of honesty.

After controlling for race and intelligence, the association between parental SES and honesty disappears, regardless of how honesty is measured (compare models 3 and 4).

Or, consider the effect controlling for IQ and parental SES have on race differences:

Before controlling for IQ/parental SES, race differences in social outcomes follow the classic White > Hispanic > Black pattern. After controlling for them, they go in different directions: Hispanics and Blacks become slightly more likely to go into high IQ occupations or get Bachelors degrees, but are still more likely to go to jail. Earnings equalized after controlling for IQ and parental SES.

Another example where regression works: wealth and fertility don’t correlate in the GSS, but controlling for educational attainment and age causes the association to reverse for both sexes:

from here

from here. Check the t-statistics

V.

My argument can be summarized simply as stating that the objections that dynomight has raised against controlling for variables could be applied to any statistical methods that are not black boxes, and that in practice, regression works well in most situations even when it is misused.

A broad trend I see within statisticians and researchers overreacting to the replication crisis by being too skeptical. In college, professors would autistically obsess over the assumptions that statistical techniques make, when in practice the only assumption violation that I have found to consistently matter is independence between cases. Besides that, determining what research is and is not true is not difficult - just mentally make the following checks:

• Is a verbal paper assessing something that is easily quantifiable? If yes, be skeptical.

• Are main p-values above .01? If yes, ignore.

• Is the main finding of the paper something that is socially desirable, consistent with the author’s political views, or their financial sources? If yes, be skeptical.

• Do the findings of a paper hinge heavily on certain citations? If yes, go leprechaun hunting.

• Are the researchers claiming a weak association based on unreliable measurements? If yes, be skeptical.

• Are variables normed to the right distributions? For example, norming a gaussian variable to a percentile distribution can cause artefacts. For example, in the following chart, the axes should be switched, and the income variable should not be forced to a percentile distribution. If a variable is normed to the wrong distribution, the non-linear associations will be biased. The linear association will usually be fine, though.

from here

• Is the author forcing a linear effect when the effect of one variable on the other is plausibly non-linear?

• An interaction effect that is over p = .001? Ignore.

• No control for genetic confounding that could plausibly be occurring? If yes, ignore.

• Did the researchers assume that controlling for polygenic scores perfectly controlled for genes? Ignore. (Exception: polygenic scores for height).

• Use of Mturk?

h/t Musa al-Gharbi

• Is the study claiming a null effect when it’s underpowered? If yes, ignore.

• Is the direction of the effect the study claiming plausibly in the other direction? Example: in panel data, autocracy and GDP per capita are negatively associated, but this is largely due to reverse causation.

• Have important confounders been addressed? In psychological studies, usually these are genes and family effect. If yes, be skeptical.

• Is a study arguing for a null effect? Chances are, regardless of their methodology, they are correct. In the modern day, absence of evidence is usually evidence of absence.

• Sample sizes?

h/t gwern

• Are the researchers claiming an association is causal based on a correlation? Ballsy, but probably incorrect. About half of variables in normal datasets are correlated. But because causality usually only occurs in one direction, and can be due to confounding with other causal relationships, a correlation will be a causal relationship maybe 20% of the time. But the stronger a correlation is, the more unlikely it is that it is due to another confounder, due to the fact that the correlation between the confounder and the two variables must be stronger than the relationship between the two variables.

• Machine learning study doesn’t use testing dataset? Red flag.

• Conclusion sounds too sensationalistic to be true? It probably is.