Joseph Bronski has hypothesized that insufficient intelligence prevents individuals from having political agency, that is, the ability to recognize and advocate for better political policies. Based on information he was able to gather, he has determined that roughly 70-95% of the population lacks political agency solely due to deficiencies in intelligence. This is inferred from the general population’s poor performance on tests of reading and mathematics — Robin Hanson and Anatoly Karlin have also observed that normal people fail to properly answer even basic questions.
There is no such thing as an item with the perfect ability to discriminate between the unintelligent and the intelligent, usually, the relationship between ability and the probability of returning a correct answer looks something like this:
Conceptually speaking, the probability of possessing the cognitive skills required to engage in political agency and IQ would be related in a similar way. This is because the cognitive skills required for political agency (reading comprehension and mathematical knowledge) are not perfectly correlated with general intelligence. The SAT could be used as a proxy for the cognitive skills required for political agency - which is what I will do in the following analysis.
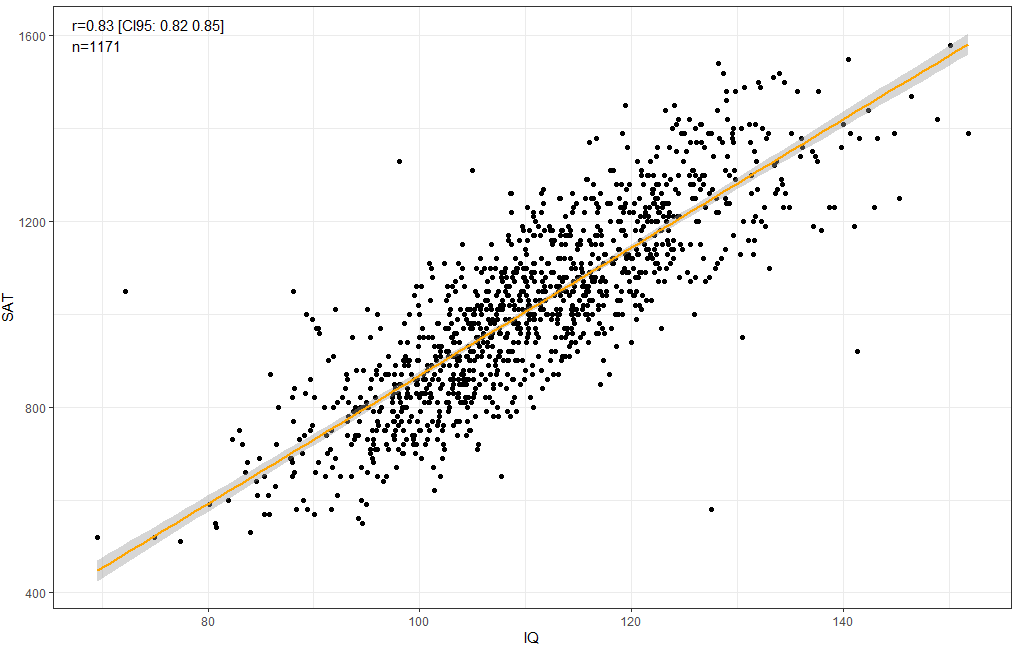
IQ and SAT scores correlate highly, but not perfectly (r = 0.84), based on my analysis of the NLSY79. This is a little higher than what Frey and Detterman found in 2004 - perhaps this is because I forced the distribution of IQ scores to a normal distribution.
It’s not clear how many individuals lack political agency due to low intelligence — estimates vary from 70 percent to 95 percent. For the sake of simplicity, 85% will be used as a rough estimate.
The 85th percentile SAT score in the NLSY79 dataset was 1100, which is an overestimate of what the nationally representative equivalent is, as more intelligent students are more likely to take the SAT in the first place. I was able to replicate this commonly held belief in the NLSY79 dataset, individuals who reported SAT scores were about 13 IQ points smarter than those who didn’t (d = 0.84, 95% CI = [0.77, 0.91]). The difference was exactly the same within only Whites, so some unobserved racial confounder wasn’t the cause of this unexpectedly large difference. Conservatively adjusting for this selection bias (multiplying by the difference by 0.84) indicates that the 85th percentile within a nationally representative sample should be roughly 940.
It appears that nationally representative studies from this time period suggested that the average verbal score was 372, and the average math score was 406.5. The SD within this dataset was 226, so the 85th percentile would correspond to an average score of 1004.
There are either two possibilities here: that my extrapolation underestimated what the true 85th percentile would be in the general population, or that nationally representative studies aren’t actually that nationally representative. I’m not sure which is the case, so I’ll average out the estimates to 970.
The relationship between the probability your SAT score is above the 85th percentile and IQ is strong, the probability an individual with an IQ score of 105 scores above 970 is just 3.9%, but for an individual with an IQ score of 130, this increases to roughly 93%.
What I am trying to explain is that there is no ‘minimum IQ’ to engage in political agency, given that the relationship between IQ and the hypothesized cognitive abilities required to engage in political agency is not perfect. Instead, the relationship between IQ and the cognitive abilities required to have political agency is logistic - high IQ individuals are much more likely to have them than low IQ individuals.
##################
NLSY97 replication:
difference between takers and non-takers: 0.9 SD
scatterplot/correlation:
85th percentile in the dataset was 1230. For the purposes of consistency, I will post two plots: one subtracted by the conventional 1100 and another with no subtraction.


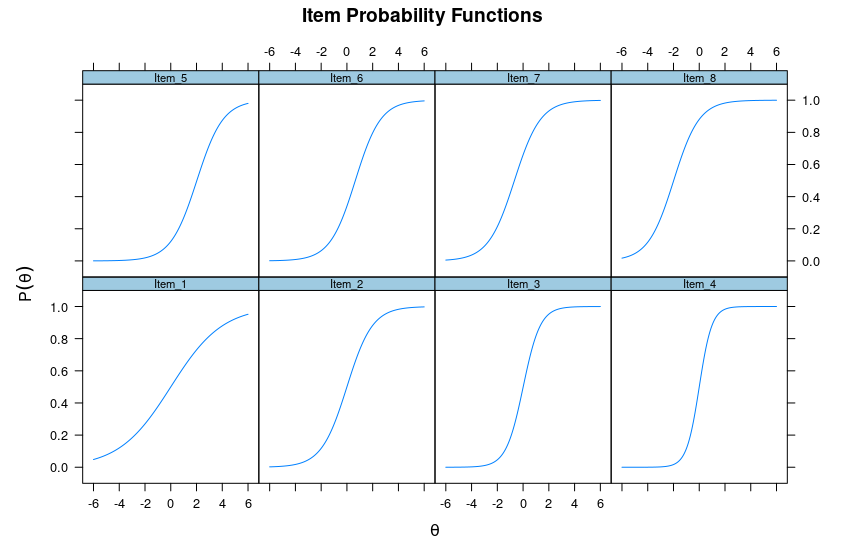





More generally, there is no minimal IQ for anything because nothing works as an item with a g loading of 1 (vertical slope). Nevertheless we sometimes put semi arbitrary thresholds for certain decision knowing these to be imperfect but useful (eg military recruits).
From which dataset is the 85th percentile 1100 vs 1230?