Taking mutational load seriously
Mutations can occur in humans due to errors in DNA recombination, radiation, or due to spontaneous reasons. The effects of these mutations can be positive, neutral, or negative, depending on the alteration made. While there is broad agreement that mutations are disproportionately likely to have negative or neutral effects on the phenotype of individuals, there is little agreement on what their net effect is. Some estimate the rate of deleterious mutations to be 2.1 per replication, while others believe it to be as high as 10.
Historically, humans have high rates of infant mortality, and it has been hypothesized that these rates keep a check on mutational load within human populations. The reasoning is as follows: there are genetic and environmental factors associated with infant mortality, and infants who die are more likely to have mutations or genes that cause mortality. If the rate at which infants die reduces, then the genes which cause these disorders will be culled from the population at lower rates.
The biggest theoretical issue I have with mutational load theory is that the more generalized mutations are, the more likely it is that mutations that cause early mortality will also cause people not to have kids, and therefore be selected out. The less generalized mutations are, the less problematic it is that mutations associated with early mortality accumulate in the population.
That aside, there are still some questions that need to be answered:
The magnitude of the effect of this change may not be large enough to cause meaningful phenotypic and genetic shifts.
Industrialization may increase the heritability of infant mortality, making the culling less frequent but more reliable.
The genes which cause infant mortality may not generalize well to deleterious outcomes in other traits. (Note: this can be used as an argument in favour of mutational load being a problem because the mutations will be selected against naturally and sexually, or against because the mutations that cause low IQ will be less likely to be filtered out because they cause deleterious outcomes for other traits).
While the last two lines of inquiry have potential, there’s not much good literature on them, so I wont comment on them in this article. That said, there is some decent evidence that decreasing infant mortality has not caused mutations to accumulate at dangerous rates. The first is that the modern French do not have more deleterious mutations than unindustrialized populations.
The association between paternal age and outcomes such as the number of children between siblings has stayed stagnant in Sweden — whether that was before industrialization occurred or after it occurred.
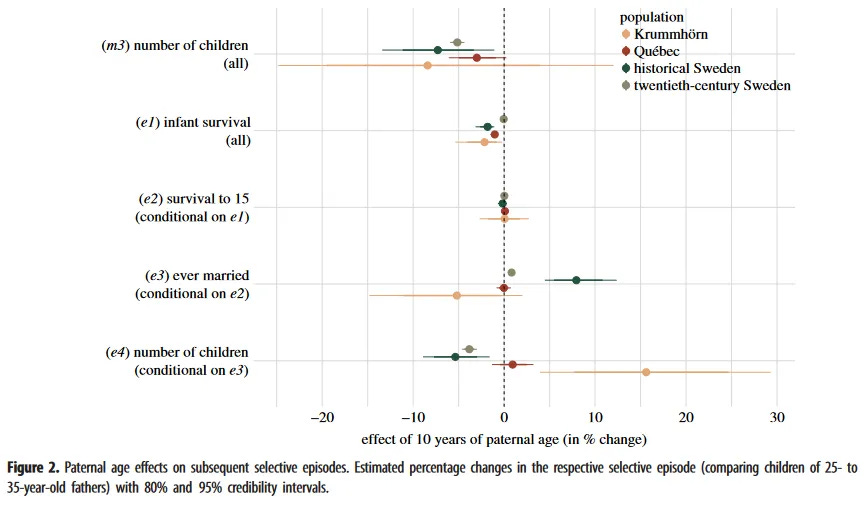
This study was the subject of a long back and forth between Woodley/Sarraf and the authors of the study:
Arslan et al. [1] found that paternal age negatively predicts offspring survival and reproductive success in four Western populations (three ‘historical’ and one ‘modern’, i.e. from the twentieth century) even after implementing controls for relevant covariates. The authors believe that this finding indicates that ‘purifying selection is still effective’ in at least one modernized population, and conclude that they ‘do not predict that contemporary reproductive timing will lead to unprecedented or unbearable de novo mutation loads and concomitant changes in the prevalence of genetic disorders' (p. 8), especially in light of the observation that average parental age has decreased over time, diminishing the number of deleterious de novo mutations added to the genomes of each new generation. We contend that negative selection acting on the relative fitness costs of mutations may be insufficient to prevent mutation accumulation in modernized populations and that the possibility of problematic increases in mutation load ought to be reconsidered.
From what I understand, Woodley/Sarraf take issue with two arguments that Arslan made:
That parental age effects should still be observed even with existing purifying selection.
That if the human genome has relied on hard selection to remove mutations, it should not be the case that soft selection can remove them.
I think both of these objections are acceptable.
Besides this, there is also a recent preprint that suggests that the effect of deleterious mutations is compensated by the effect of beneficial mutations, which explains why we haven’t died 100 times over due to mutational load, as Kondrashov noted in 1997. Admittedly, I don’t know much about this particular field of research, and am skeptical of simulations in general, but I figured it would be worth mentioning.
“Each new human has an expected Ud =2 - 10 new deleterious mutations. This deluge of deleterious mutations cannot all be purged, and therefore accumulate in a declining fitness ratchet. Using a novel simulation framework designed to efficiently handle genome-wide linkage disequilibria across many segregating sites, we find that rarer, beneficial mutations of larger effect are sufficient to compensate fitness declines due to the fixation of many slightly deleterious mutations. Drift barrier theory posits a similar asymmetric pattern of fixations to explain ratcheting genome size and complexity, but in our theory, the cause is Ud >1 rather than small population size. In our simulations, Ud ∼2 - 10 generates high within-population variance in relative fitness; two individuals will typically differ in fitness by 15- 40%. Ud ∼2 - 10 also slows net adaptation by ∼13%-39%. Surprisingly, fixation rates are more sensitive to changes in the beneficial than the deleterious mutation rate, e.g. a 10% increase in overall mutation rate leads to faster adaptation; this puts to rest dysgenic fears about increasing mutation rates due to rising paternal age.”
There is also the issue of birth order effects — if earlier birth orders have a causal effect on certain phenotypes due to environmental reasons, then that will inflate observed parental age effects. This is because parental age effects to become correlated with certain traits, not because of mutational load, but because parental age will correlate with birth order.
Children born earlier in the family tend to have higher GPAs, and this effect is much larger within families than between them. This suggest that the lion’s share of the effect is driven by the environment, not genetic factors like mutational load or correlations between fertility and traits at the population scale.
The effects are also not culturally invariant — birth order effects only exist for ethnic Norwegians, not other ethnic groups. (Note: none of the effects within other ethnic groups reach statistical significance).
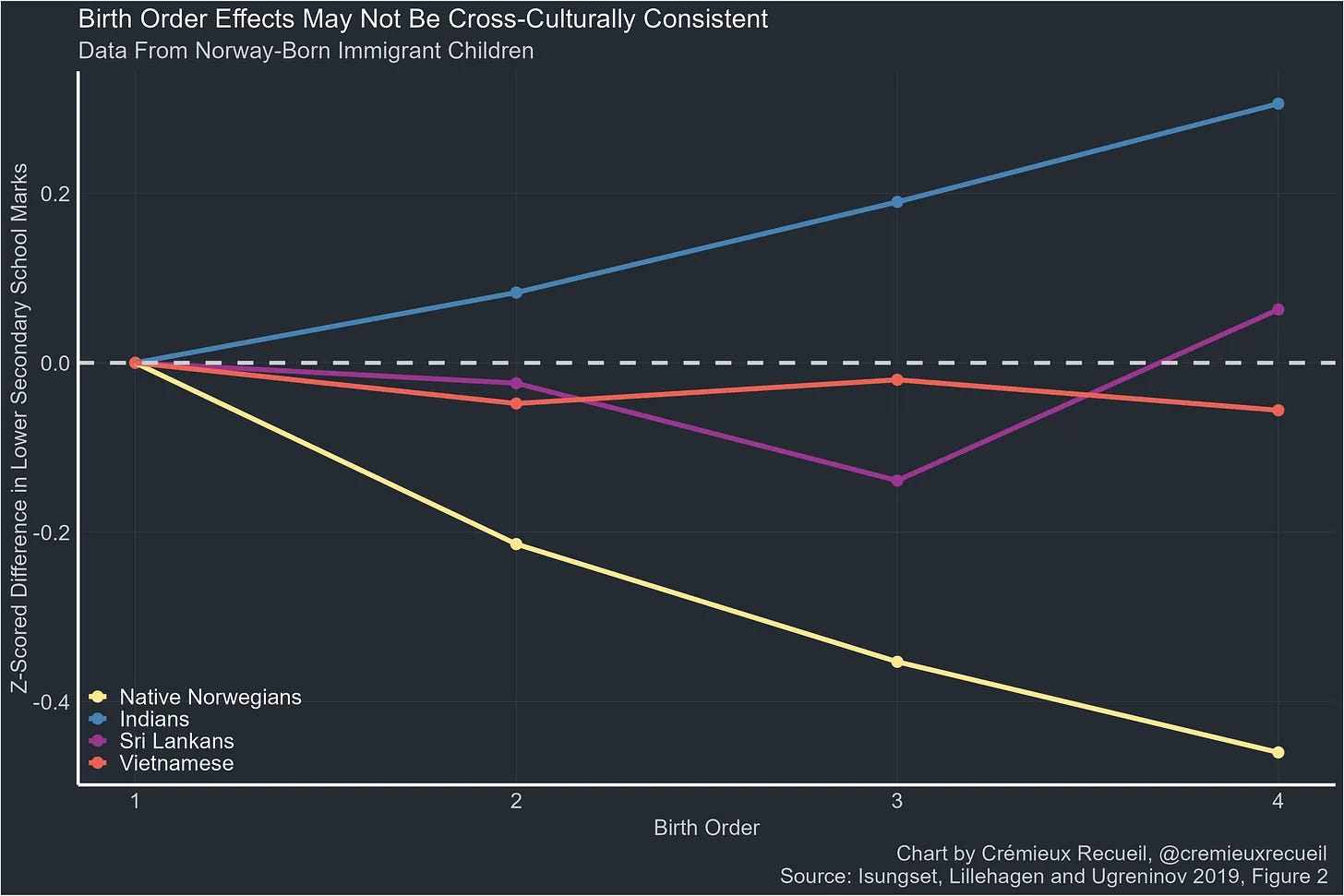
Birth order effects for educational attainment also exist for adoptees, which suggests an environmental effect, not a genetic one.
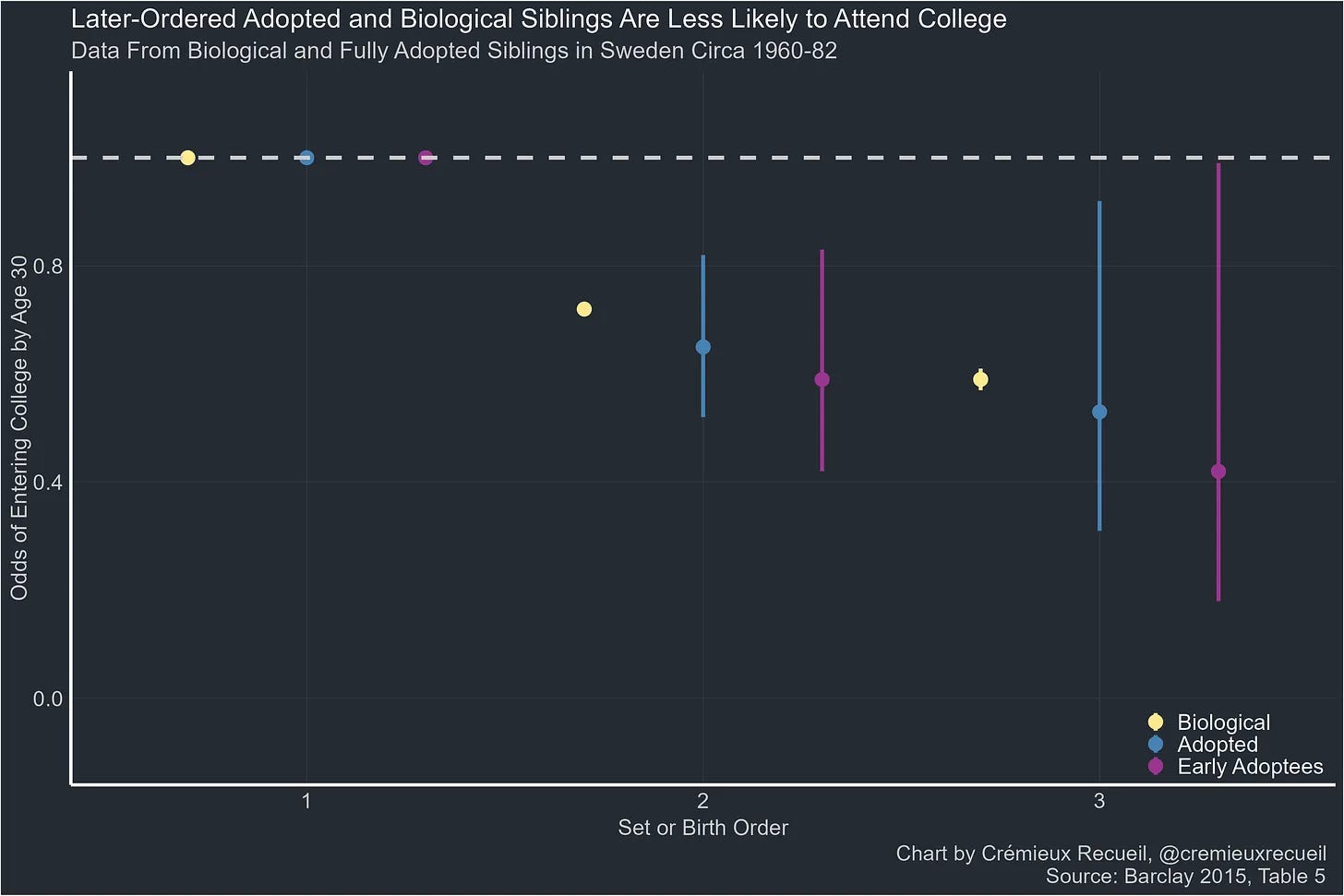
When families are split into three types: multipartnered mothers, multipartnered fathers, and nuclear families, the birth order effect for school grades only exist for the multipartnered mothers and nuclear families. Again, this evidence strongly suggests that the origin of the birth order effects are environmental, not genetic.
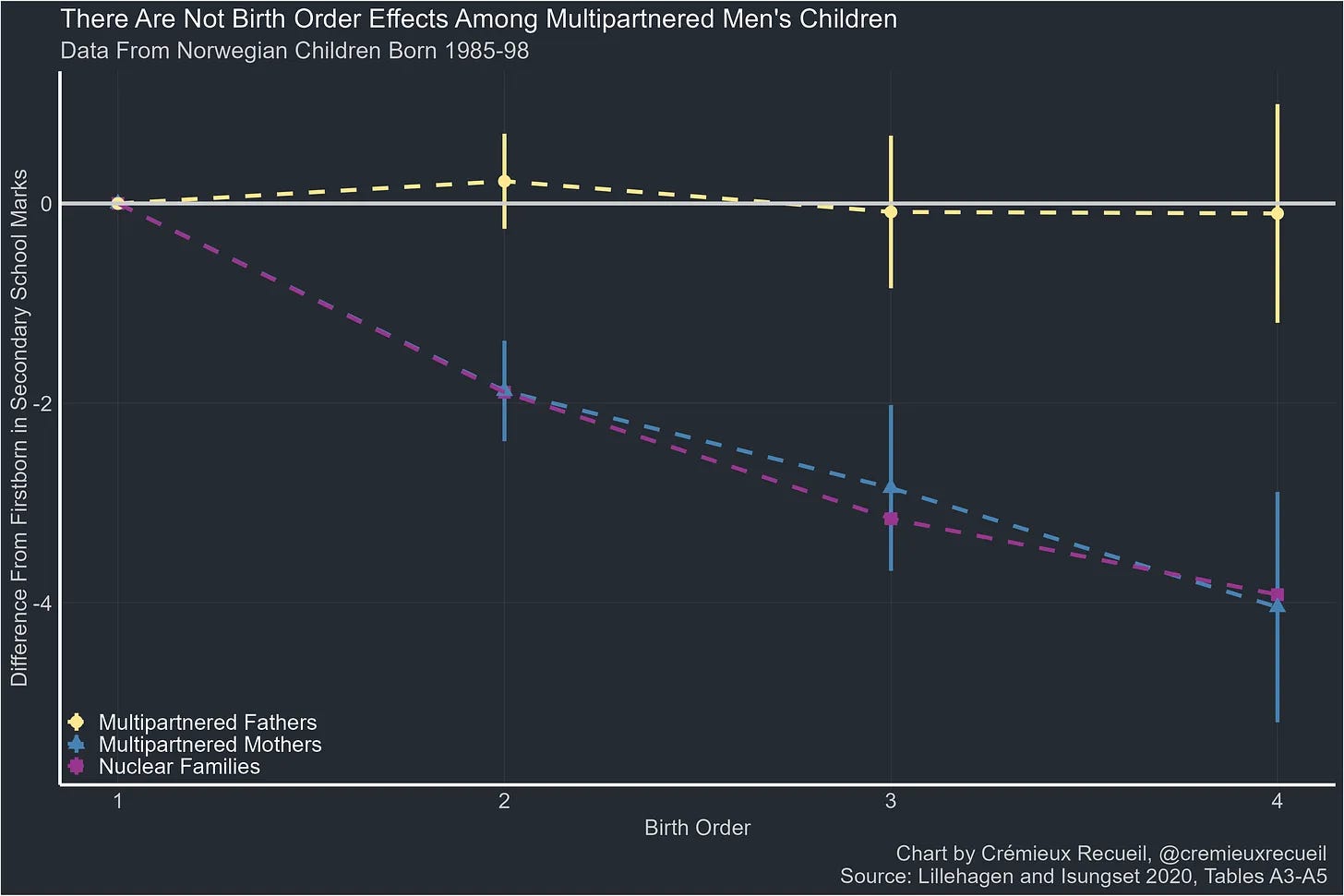
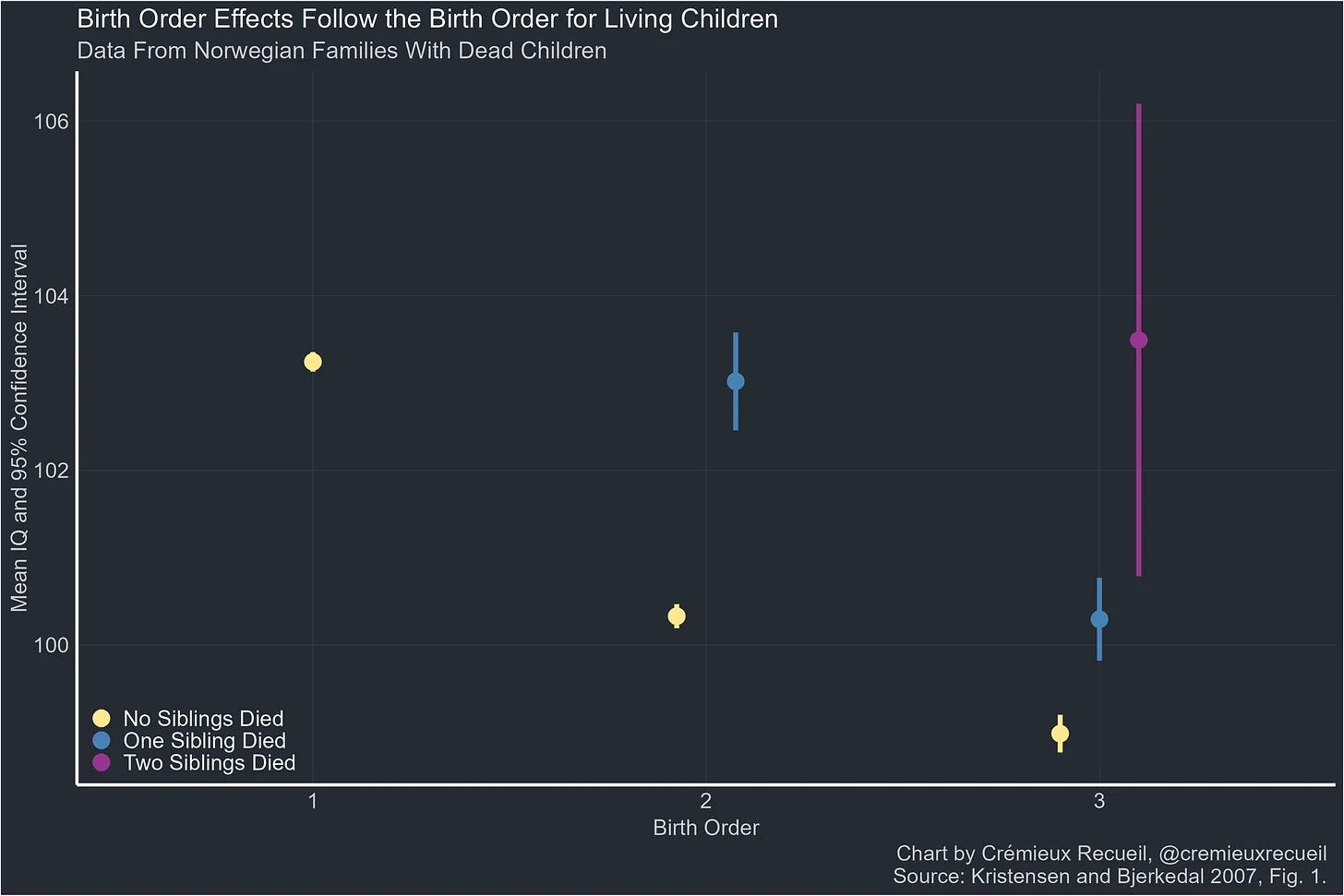
There are also birth order effects for intelligence — earlier born children are more intelligent than the later-born ones. When a sibling dies, the averages are consistent with the social order, not the birth order.
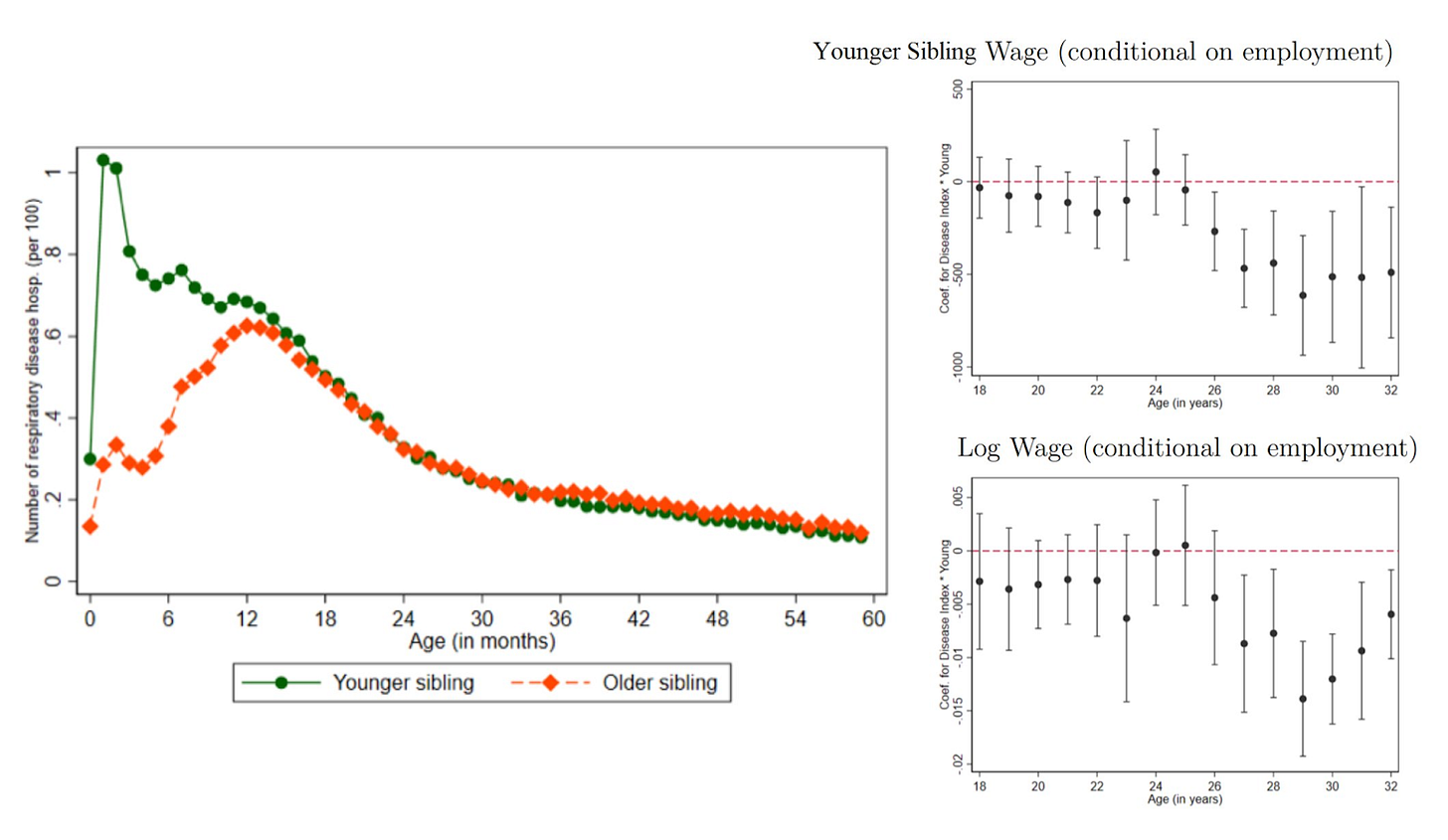
As for concrete environmental influences, one of them is potentially infections: younger siblings are more likely to get respiratory infections because of interactions with their older siblings, those infections stunt their development, and they go on to gain lower wages.
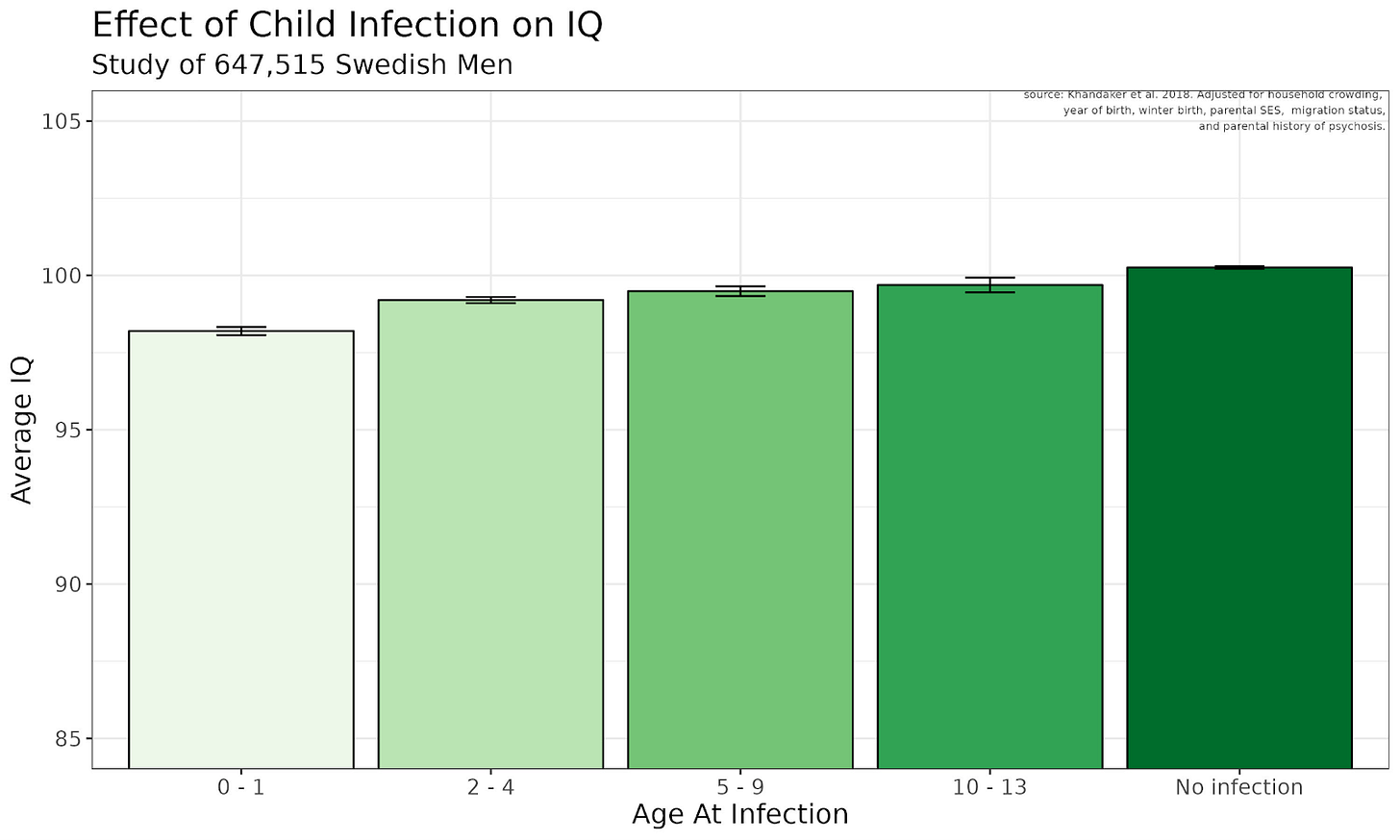
This effect also replicates in large samples - Swedish men who are hospitalized from infections score lower on military entrance exams, and this is especially true for those who got infected at younger ages. Admittedly, this could also be explained with reverse causation, where less intelligent children go on to become infected, though this doesn’t explain the absence of the effect at older ages.
Genetic evidence of mutational load
If mutations in genes that are causally associated with a trait tend to be deleterious, then the association between allele frequency and effect size should be positive. If there is no association, that could be due to a combination of factors - perhaps the purifying selection is too strong, or the effect of mutations on the direction in which the trait is expressed is too weak.
For height, there is no association between minor allele frequency and effect size - 48% of rare variants increase height, and 52% of them decrease height. It is probable that the true relationship within the entire genome between allele frequency and effect sizes is positive, as dwarfism is more common than gigantism, though there is no way of knowing for sure.
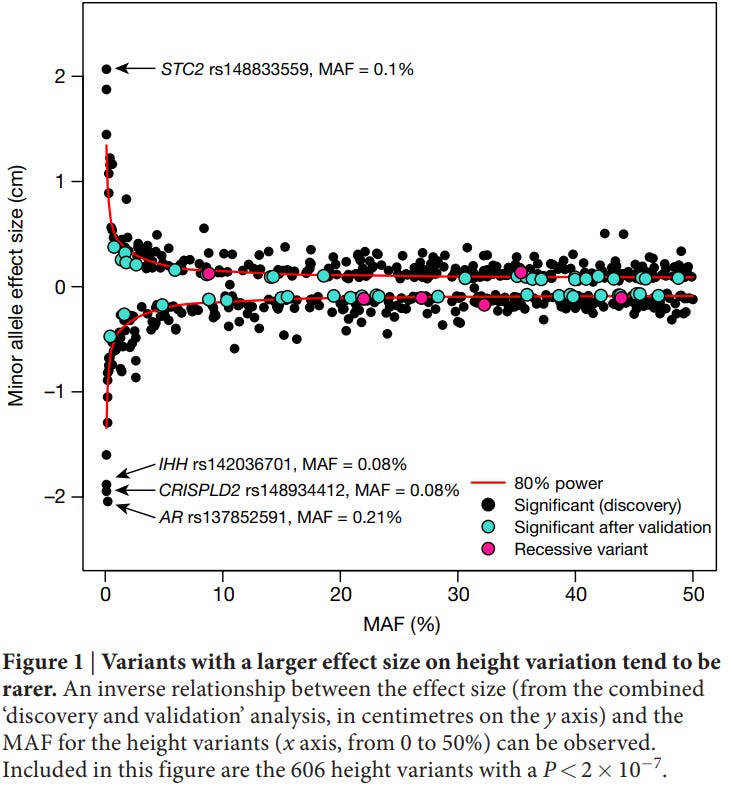
For educational attainment, rare variants that are genome-wide significant have disproportionately negative effects.
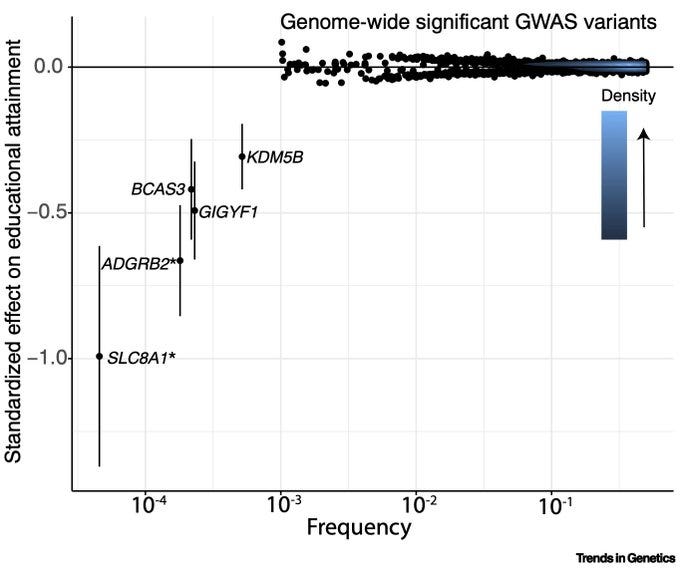
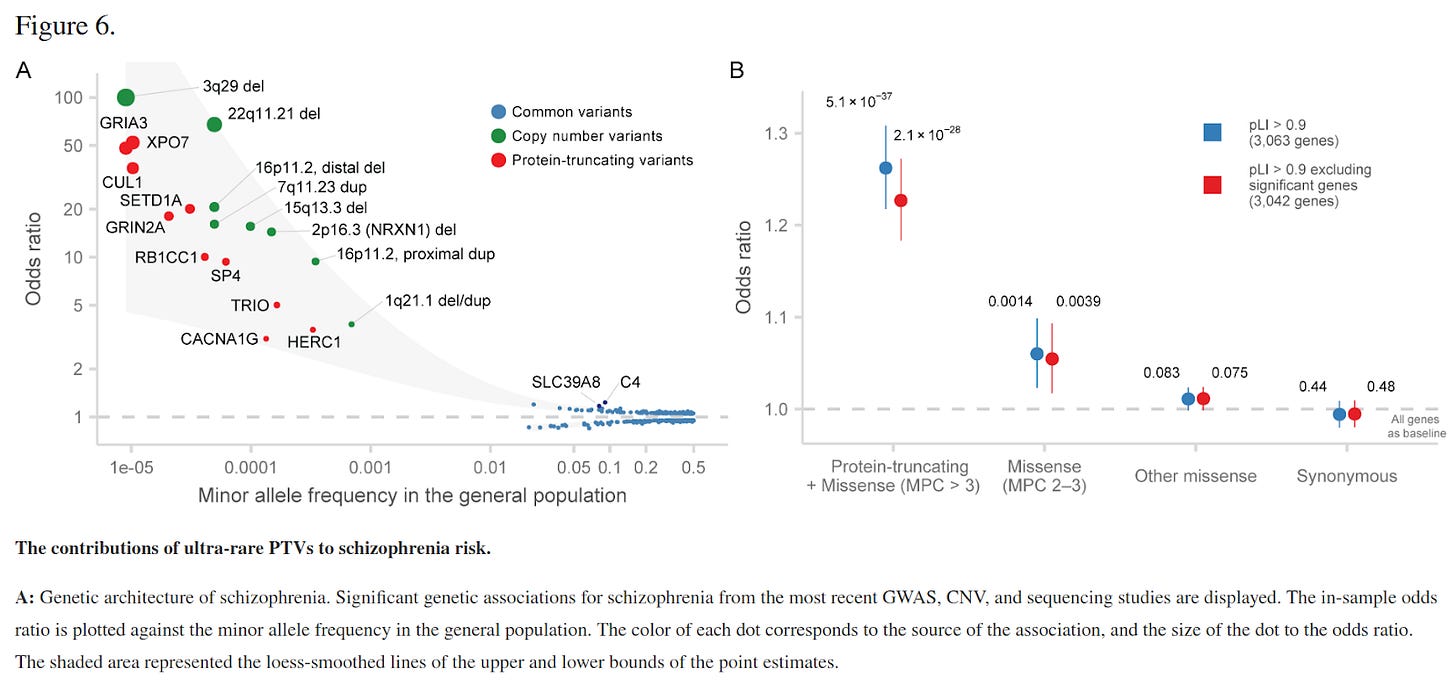
For schizophrenia, rare alleles and protein-truncating variants were disproportionately causal for higher rates of schizophrenia. These alleles were also likely to cause autism, epilepsy, and other severe neurodevelopmental disorders.
Mutational Load and IQ
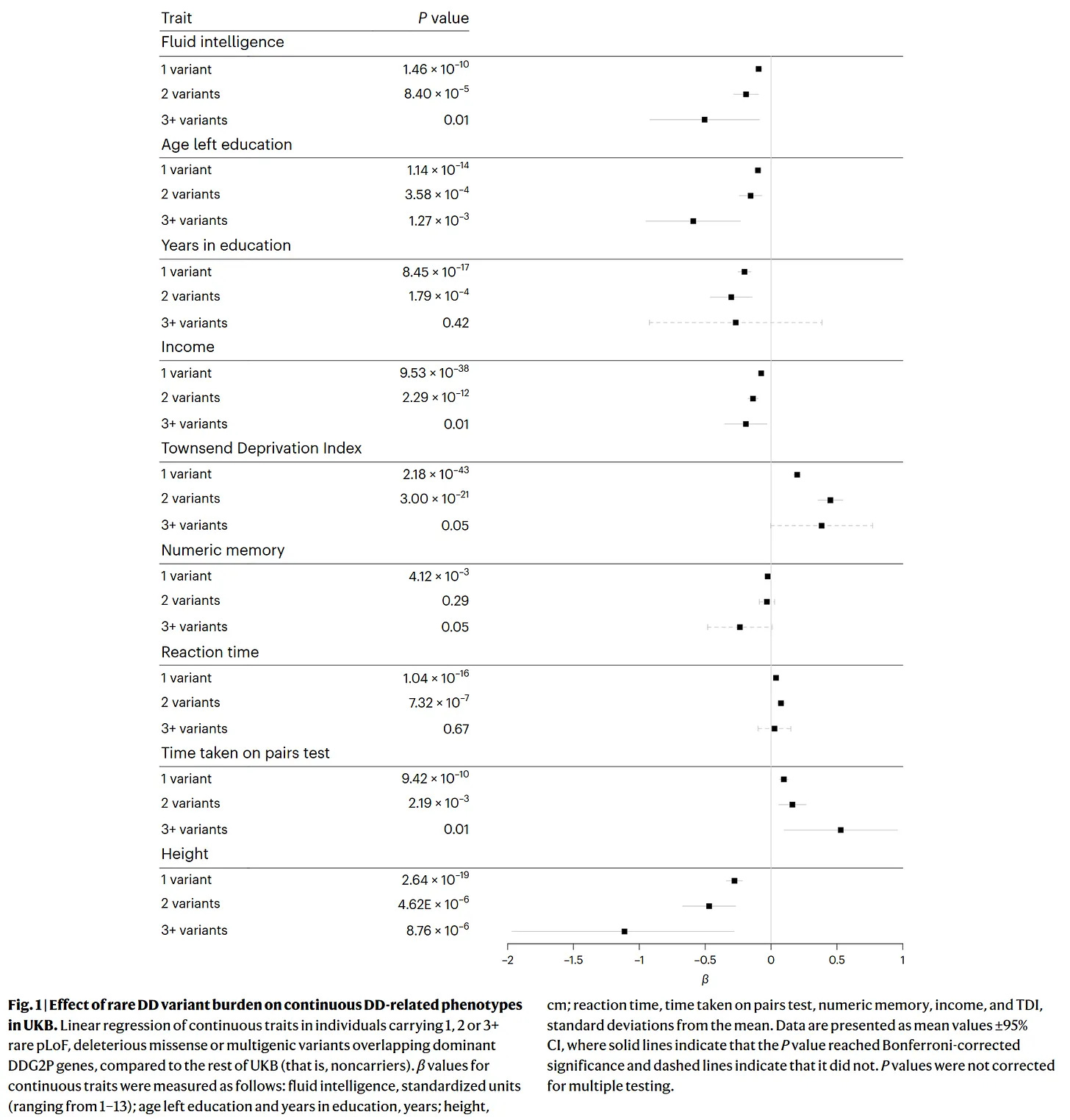
Rare alleles disproportionately lower cognitive ability, meaning that if mutations occur, they are going to lower cognitive ability. Given that polygenic scores for intelligence have increased over time in Europe, and that humans still have their heads attached to their necks, we can be fairly confident in knowing that in the unindustrialized environment there are ways that these mutations are dealt with, whether it is purifying selection, sexual selection, or natural selection. Intelligence is typically associated with lower levels of completed fertility (see Woodley’s meta or mine), this should cause the average level of cognitive ability to decline by about 3-4 points per century.
This on its own is concerning, but could possibly be fixed with genetic engineering technologies or a gradual reversal in the relationship, which is likely given that the correlation between educational attainment and fertility is decreasing in magnitude over time.
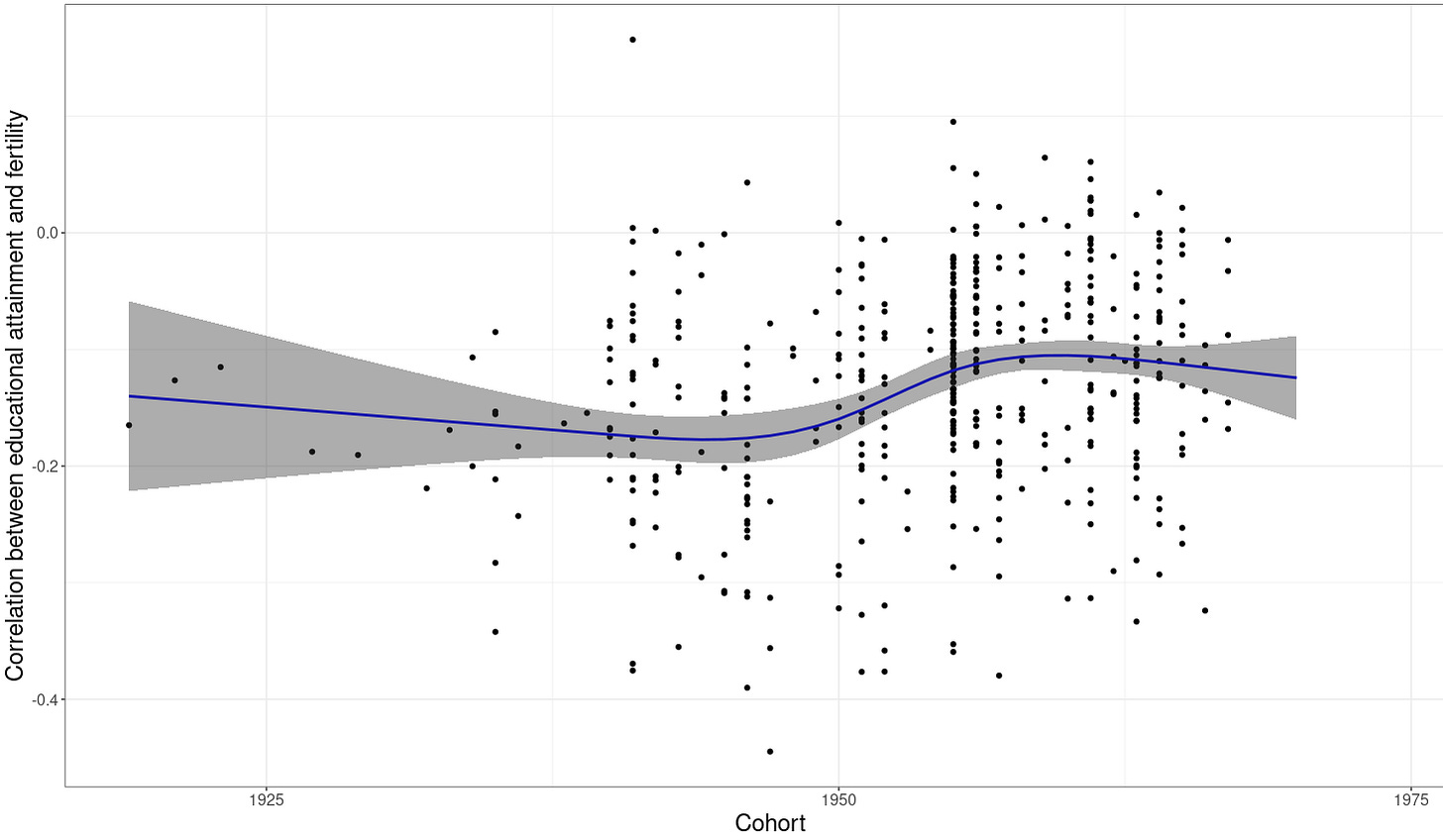
What would be more concerning is if the lack of purifying selection were to cause mutational load to gradually accumulate and cause intelligence to deteriorate. At the moment, the leading advocate of the hypothesis that intelligence is declining due to mutational accumulation (Woodley) currently estimates the decline in heritable intelligence to be 1.6 points per century.
While it is correct that IQ scores have increased across time in the west, this effect does not generalize to all cognitive tests. Scores on tests of fluid reasoning (such as the raven’s matrices test) have increased massively, while scores on crystalized tests have been fairly constant since the 1980s.
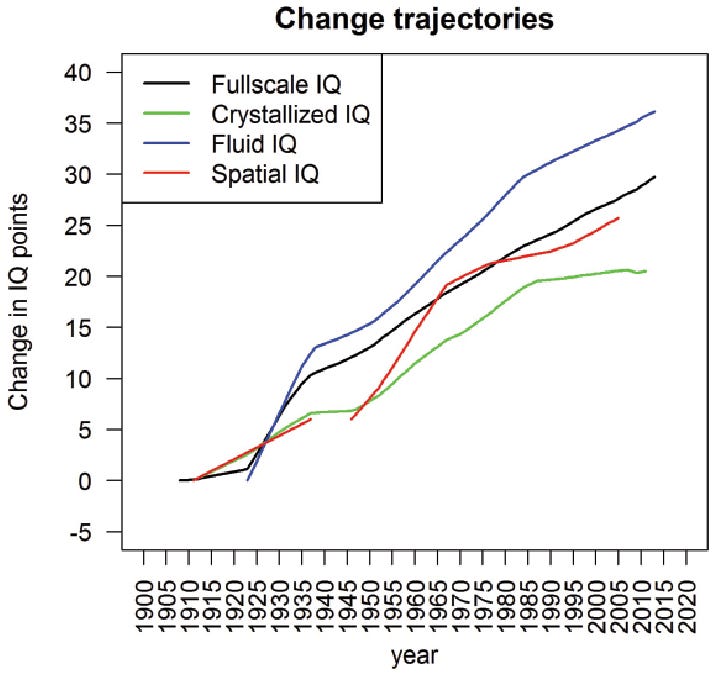
Within the United States, the performance of students on the NAEP standardized tests has not changed very much in the last 50 years.
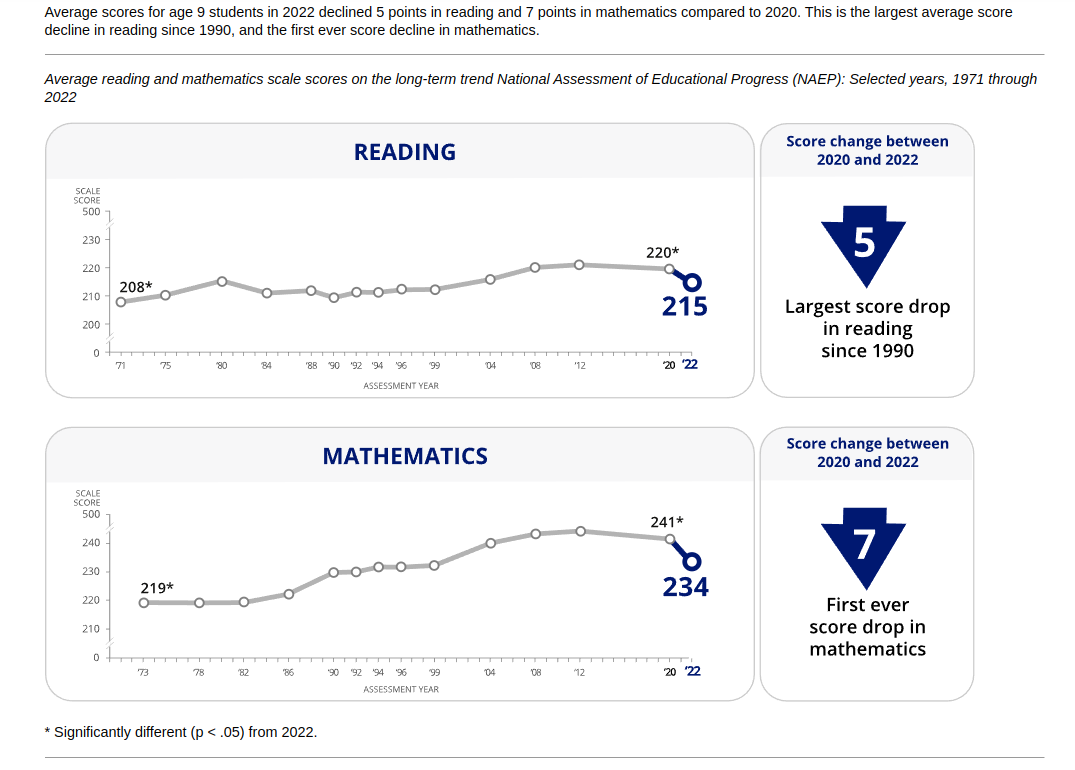
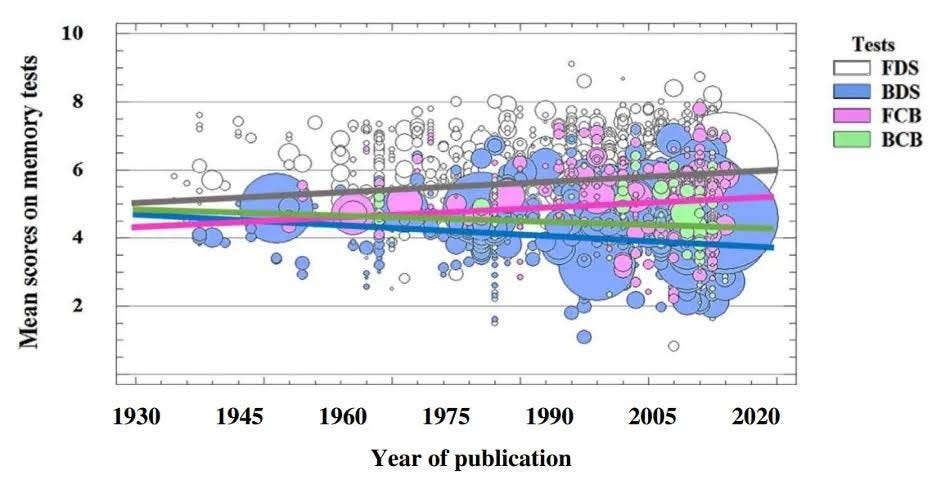
According to the meta-analysis, the drop in backward digit span scores was the equivalent of about 2.13 points per century. The decline in backward corsi block span was 5.82 points per century, though this figure is more unreliable as it is based on less individuals (n=3,784) than estimate from backward digit span (n = 70,424). These tests have the advantage of being the ones that, based on priors, are least likely to exhibit bias across time, so it’s plausible that the true decline in intelligence that has occurred in the last century is within this range.
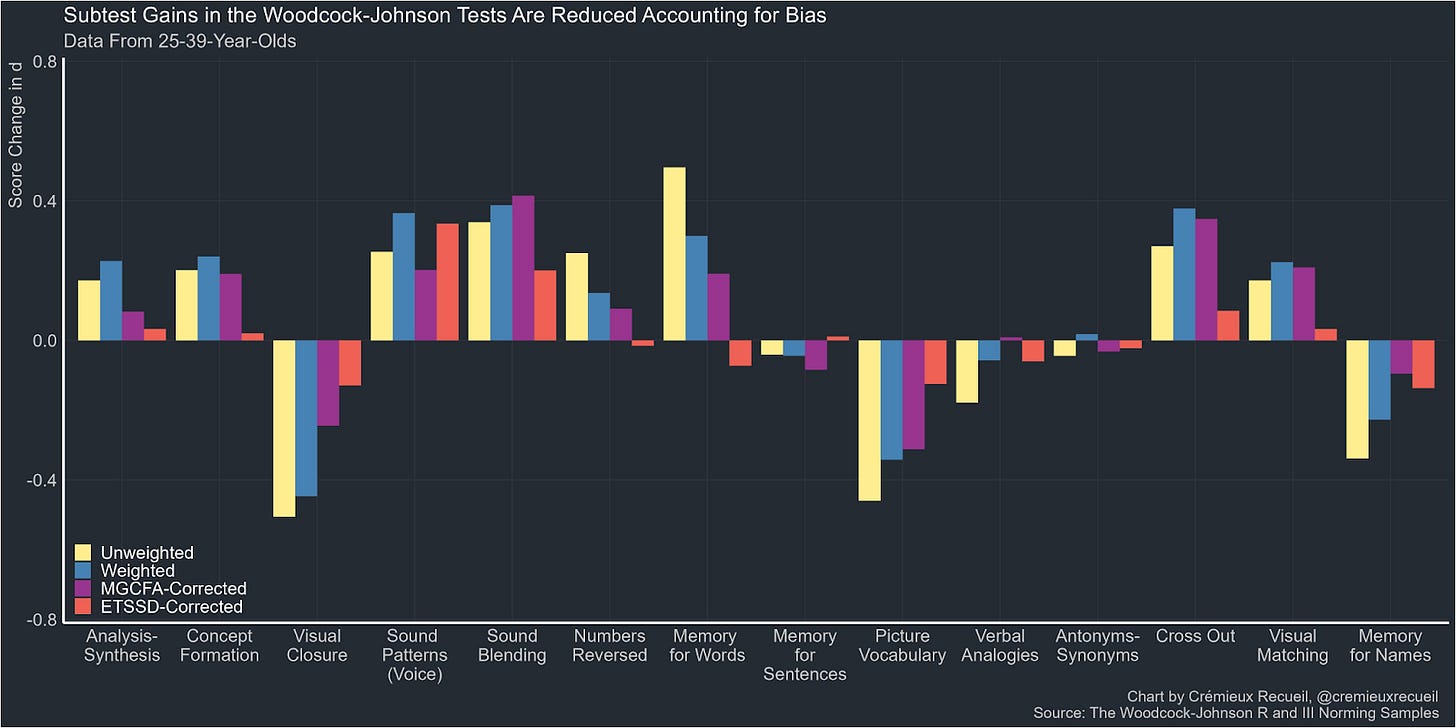
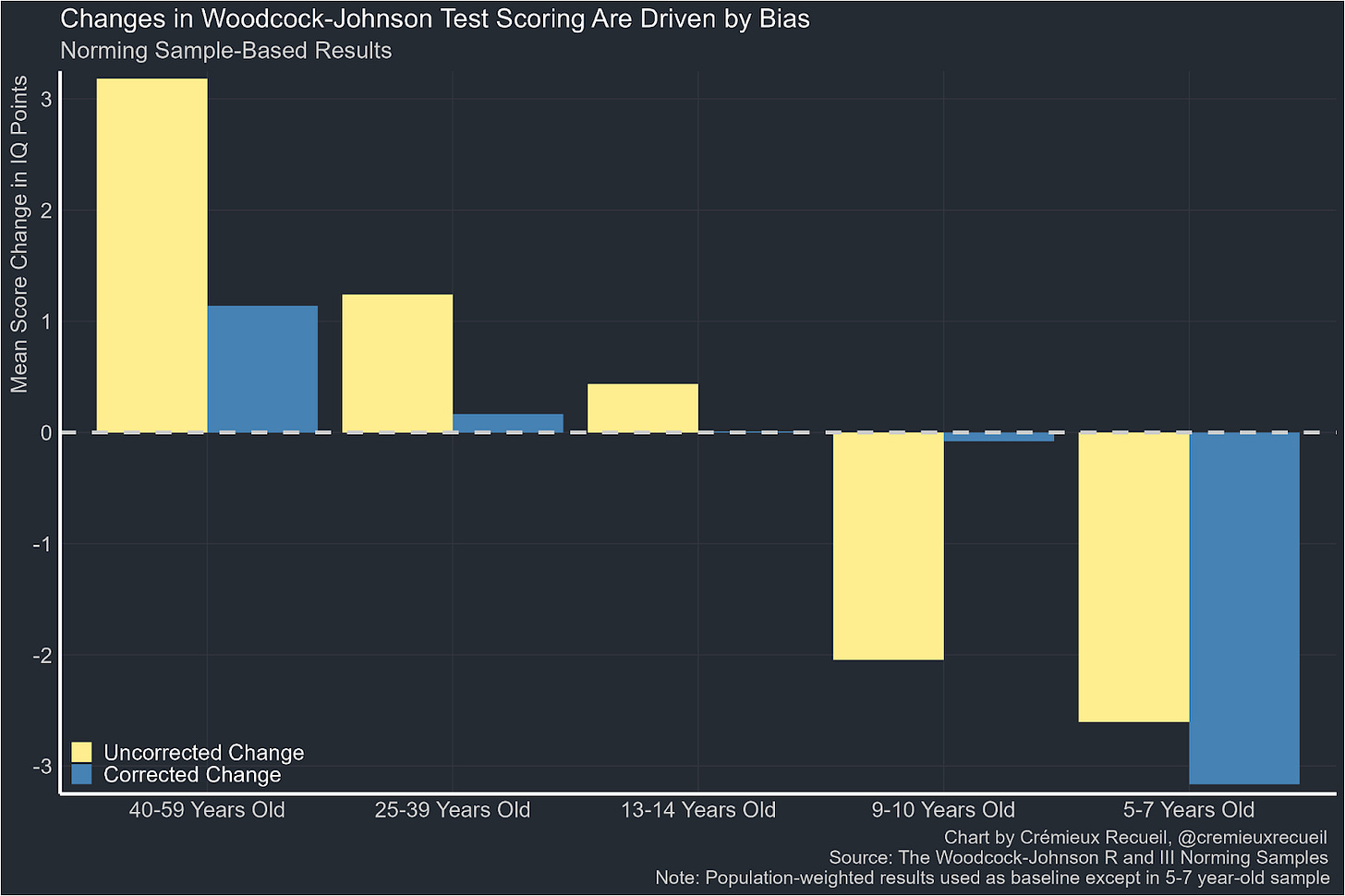
There are also studies that examine whether changes in performance in IQ subtests are sensitive to corrections for measurement invariance, which suggest that both declines and increases on the Woodcock-Johnson IQ subtests between 1987 and 1999 appear to be due to test bias, with the notable exception being the ability to recognize sounds.
This effect also exists when the overall scores are measured.
Besides this study of the Woodcock-Johnson, this reddit user summarized the state of the research on measurement invariance between cohorts for intelligence well:
Analysis of the Dutch WAIS and Differential Aptitude Test (DAT) clones by Wichert in 2004. Measurement invariance failed between cohorts.
Dissertation on the Flynn effect which examined changes in the College Basic Academic Subjects Examination (CBASE) over time. Author found evidence that the change in scores over time was sensitive to methodology, where classical test theory found larger gains than IRT based models.
A study of the NLSY which found no gain in the PPVT-R and PIAT-M subtests after controlling for measurement invariance.
The studies of the Estonian data are heterogeneous in terms of results, but most studies seem to agree that the gains are affected by psychometric artefacts.
Scores on the GSS WORDSUM test have not changed after accounting for psychometric bias using IRT models based on a study by Beaujean in 2010.
A study of changes over time on the SAT and ACT found that measurement invariance across years was violated.
He also cites six more studies which find evidence of violations in measurement invariance across time, though it would be overkill to describe them all. So I’ll just post the links to all of them. [1], [2], [3], [4], [5], and [6].
II.
Beyond the issue with measurement invariance, a meta-analysis done by te Nijenuis finds that the Flynn effect is concentrated in the least g-loaded tests (r = -.38), meaning that it is unlikely that the observed increases in cognitive test performance reflect gains in overall ability.
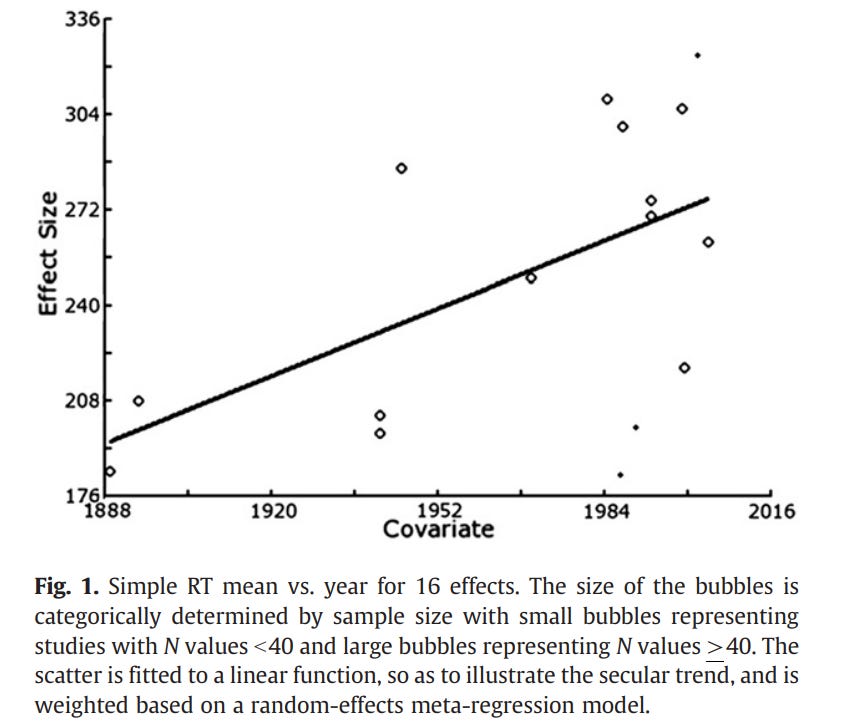
While most cognitive tests find increases in scores across times, Woodley has found several cases of cognitive tests that find decreases across time. The first is a meta-analysis of reaction time that finds a decrease of 12 points per century (note: I doubt Woodley would endorse this figure as a precise estimate of the decline in intelligence). This study has been criticized on multiple grounds, notably that:
The meta-analysis itself is small, and includes few studies from before 1950.
The two studies from before 1900 come from selected samples: some people who visited a museum and students from the University of Chicago.
There are some other criticisms of this meta-analysis: that the increase over time has to do with changes in hardware or racial composition.
It is still worth commenting that the effect is still in the expected direction, and larger studies that lack sampling bias do still show some slowing. A different study on secular changes in reaction time found a decrease within women, but not men, with an estimated decline of 15 points per century within women. This is somewhat concerning, as the effect of selective breeding and mutational load should not vary by sex. I suspect this result is due to awkward modeling, where they try to estimate three curves using only six data points.
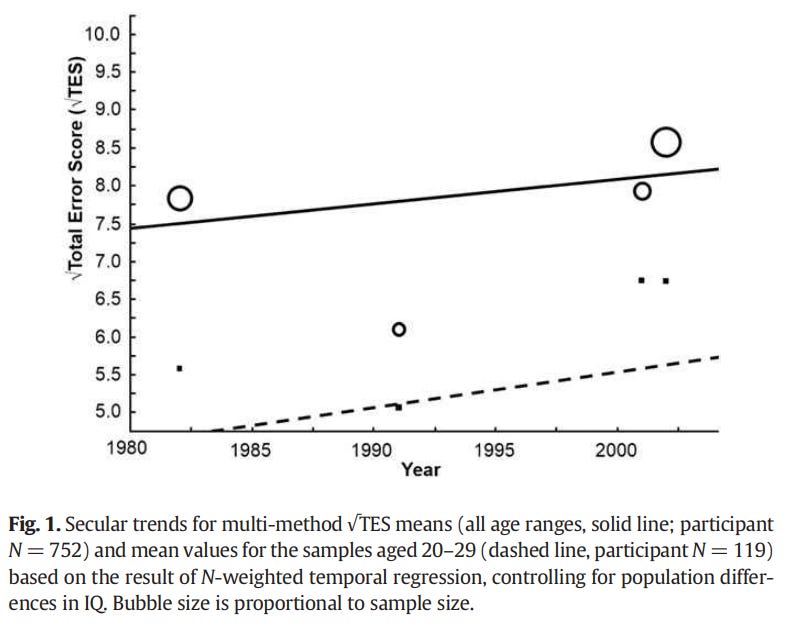
Besdies the reaction time studies, there is also a hue discrimination meta-analysis that finds a decline in performance of 22 points per century, which Woodley does not think is due to genes. It has similar issues to the reaction time meta-analysis — there are few datapoints, and four of the datapoints on the lower end of the plot are based on the younger samples of the larger studies (though this was intended as a robustness check, not an additional sampling point).
There is also the issue that rare variants that cause developmental disorders have a much smaller effect on reaction time in comparison to cognitive or social traits. That calls into question whether mutational load could even cause declines in reaction time performance of almost an entire standard deviation per century if the absence of purifying selection was an issue.
Some have argued that the recent negative Flynn effects are evidence of accumulation due to mutations — they are too large to be due to mutational load. Even according to the most pessimistic estimate (decline of 1.2 SD in IQ per century in genotypic IQ), only two of these declines could be plausibly due to mutational load.

The decline in Norway is underestimated due to the fact that the selection for cognitive ability when taking military entrance exams increased, and controlling for this causes the decline to increase even further (~3 points per decade).
There is another study that finds that IQs have decreased in the United States — this is due to poor statistical methodology. The finding is an artefact of controlling for educational attainment, which is becoming less selective over time, so IQ scores decline within education categories, but not between them. See Emil Kirkegaard’s analysis here.

Woodley himself has argued that the negative Flynn effects are not consistent with changes in mutation accumulation in his book The Rhythm of the West: he found that the strength of the effect was weaker in more valid tests of intelligence, and that immigration predicted declines in IQ, which is consistent with declines in PISA performance in Finland.

III.
There are also concerns over the decline in innovation per capita, which people have used as evidence for a decline in intelligence. I don’t find this particularly convincing: these changes can be affected by anomie or the picking of the low hanging fruits.
IV.
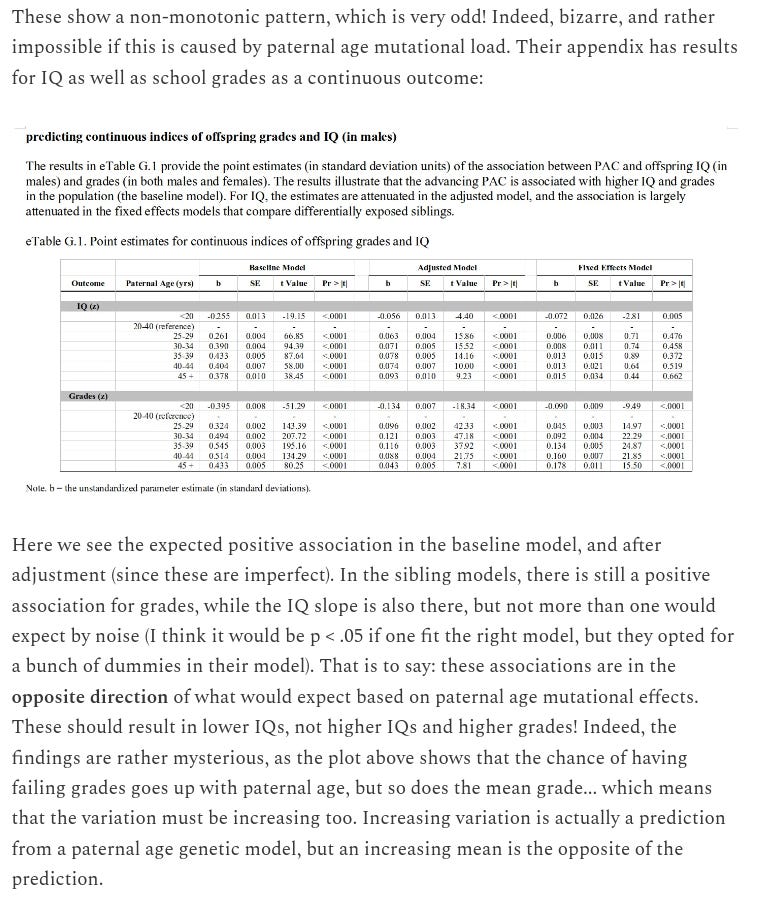
There are also a few studies that attempt to evaluate the effect of mutational load on IQ using parental age estimates. The first one I found was cited by Woodley’s meta-analysis, and finds a non-significant negative effect (b = -.015, 95% CI [-.065, .035]) of parental age on IQ when controlling for birth order. Woodley thinks that the estimate that doesn’t control for birth order should be used because the effect may be mutagenic, though it was shown earlier that birth order effects are environmental, not genetic, so control for them is necessary.
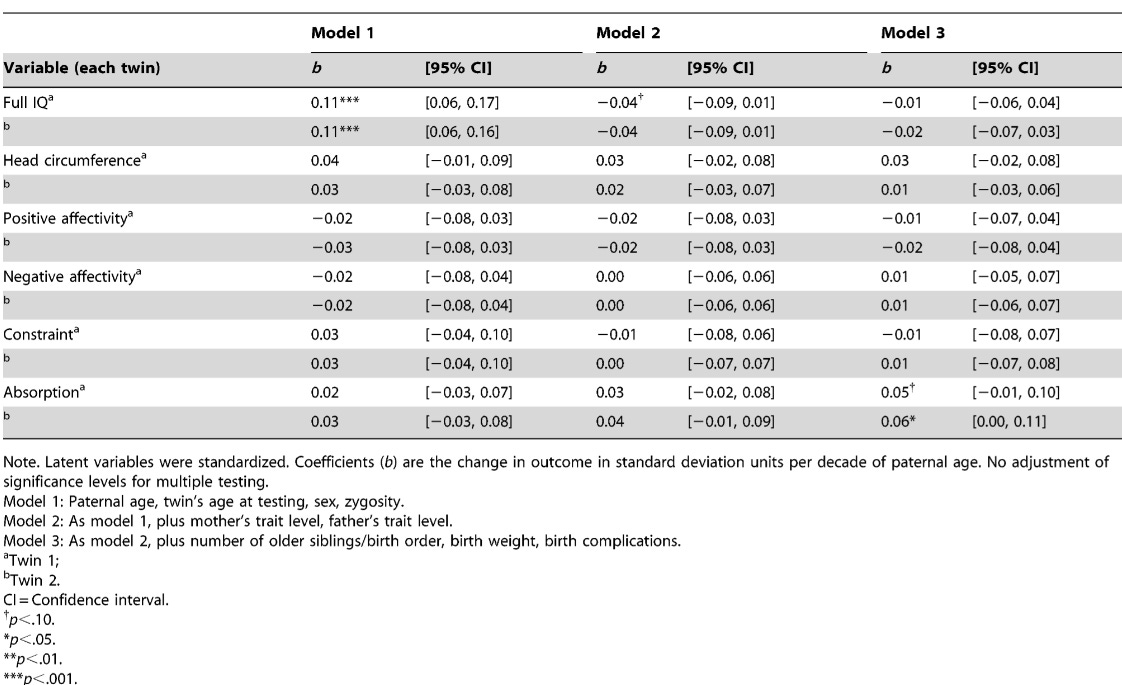
A second study on parental age effects on IQ comes from Wang (2023), who finds an effect of parental age on IQ before controlling for birth order, but a non-significant negative effect after controlling for it:
The association between parental age at conception and children's traits has often been studied as it may reflect germline de novo mutation accumulation and is expected to be monotonic negative. However, for IQ, the relationship has often been found to be inverted U-shaped, possibly because of confounding by parental characteristics that correlate with child-bearing age. Here, I leverage polygenic scores (PGS) as an indirect measure of parental intelligence and examine how the effect changes as the explanatory power increase to heritability. Heritability can be estimated by calculating the phenotype variance explained by the genetic effect when the paternal-maternal ratio of the projected age effects after controlling the genetic effect matches the male-female ratio of mutation rate. After controlling for PGS and demographic factors, I estimate a −2.0 (95 % CI, −0.3 to −3.7) IQ points change in intelligence per decade rise in paternal age. After further adjustment for birth order, it declined to −0.6 (−2.6 to 1.6). Even if only the latter estimate is attributable to mutation accumulation, the result would imply a substantial contribution of de novo mutations in the variance of intelligence. However, the association might not equal the effect of de novo mutations and further studies are needed.
He uses PGS scores to control for parental IQ — this is better than nothing, regardless, these results shouldn’t be taken too seriously. To account for the fact that PGS don’t account for all of the variance in intelligence, he adjusts for the imperfect heritability of the measurement:
There is a gap between the largest variance explained by PGS (9.7 %) and the family-based heritability (at least 50 %), which means controlling for any of the available PGS is not enough to take account of parental confounding. Because it is the phenotype that directly influences the age at reproduction, the underlying genotype, no matter whether captured by PGS or not, should influence the age at reproduction in the same way. Therefore, when the variance explained matches the full heritability, we can take the projected value of the effect as the true effect of increasing parental age. Similar approaches were employed in earlier studies (Beauchamp, 2016; Pingault et al., 2021). However, how much exactly should the heritability be taken? We can take advantage of the fact that the ratio of de novo mutation rate between males and females is known and the relative strengths of paternal age and maternal age effects should match the ratio. When they match, the proportion of variance explained is a new estimate of heritability. When estimating the effects, heritability estimated in this way was used.
Besides these two studies, I found two attempts to evaluate the effect of parental age on IQ. Both had positive effects, one statistically significant and the other was not. The first is from a Swedish paper that evaluated the effect of parental age on various traits with a large sample, and found a statistically significant positive effect in their siblings fixed effects model. They adjusted for birth order, according to the main body of their paper, so that effect should not be an issue.

V.
Unfortunately, the parental age studies are a dead end because extraordinarily large samples and high quality controls are needed to estimate the effect precisely. Because of that, I’m going to try to give a theoretical argument as to why mutational load cannot be decreasing intelligence by large amounts across time. Consider the following mathematical formula:
IQ can change across generations within a population because of either genetic and environmental factors. These genetic factors can be either due to differential fertility or mutational load, and these environmental factors can be due to real increases or illusory ones (e.g. psychometric bias).
We can already start filling in some of the blanks. In change per century notation (which is what I like), the coefficient of differential fertility should be -3.5 points per century according to my meta-analysis, and the change in observed IQ is 28 points per century. This leaves us with:
For now, I will assume a decline of 8.4 points per century in mutational load.
Between the psychometric bias and real environmental gains, 40 IQ points have to be found. That seems implausible. There were the earlier studies that suggested that FE gains were affected by psychometric bias, but not to that extent
VI.
The current method of estimating the effect mutagenic dysgenic effects on population level phenotypes is estimating the causal effect of parental age (e.g. decrease of 2 units per year of paternal age) and then multiplying that by 100 to obtain the expected change per century (200). This model works, and only if, there is zero purifying selection for deleterious mutations. It does not if there is selection against these mutations due to sperm selection, miscarriages, infant mortality, natural selection, sexual selection, or genetic drift. While the purifying selection against mutation is probably falling in infants, it is unclear how much this translates to other selection mechanisms.
Notably, mutations that cause schizophrenia also cause autism, epilepsy, and other neurodevelopmental disorders; this is also the case for mutations that cause developmental disorders also cause lower income, cognitive ability, and educational attainment. Fluctuating asymmetry, an indicator of mutational load, appears to be a fairly robust indicator of poor fitness in a wide variety of traits:

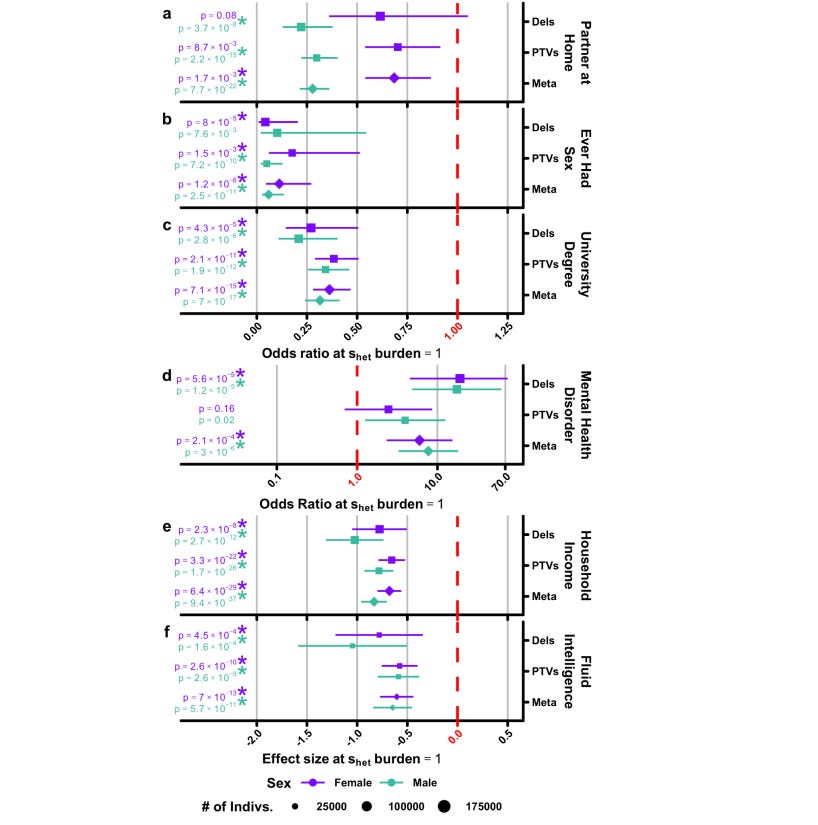
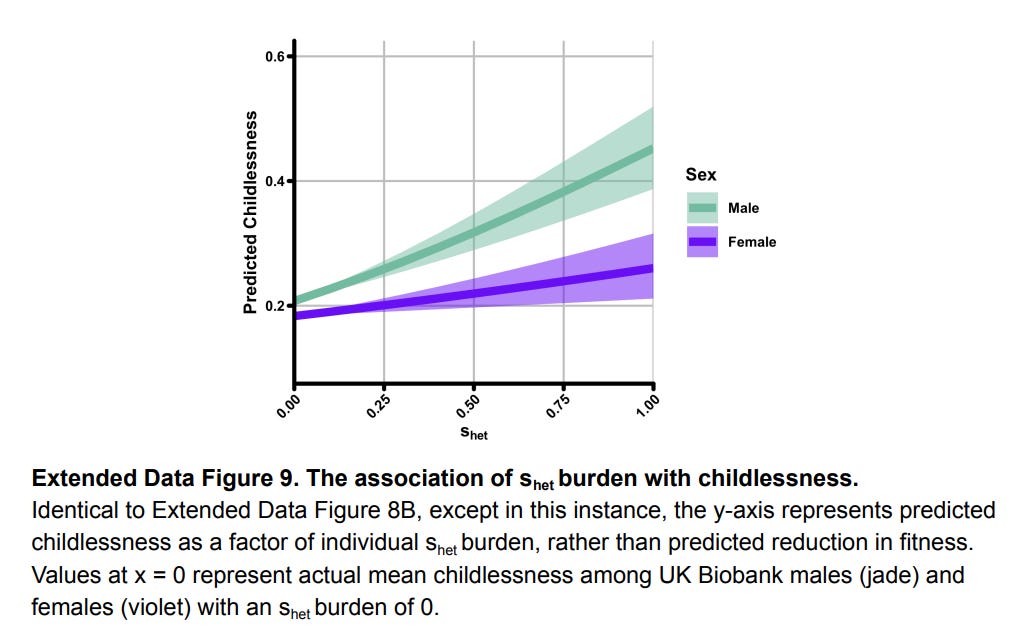
Mutations that cause lower levels of intelligence will not be selected against due to their effect on IQ, as IQ is being selected against in modern populations, but if these mutations have negative effects on traits that are positively selected for, then they will be less likely to be transmitted to the next generation. This may appear to be the case according to data from the UK Biobank - mutational load decreases the odds of having sex and having a partner at home, particularly for men. This appears to translate to lower levels of fertility, particularly for men (men — green, women — purple).
Mutational load and psychopathology
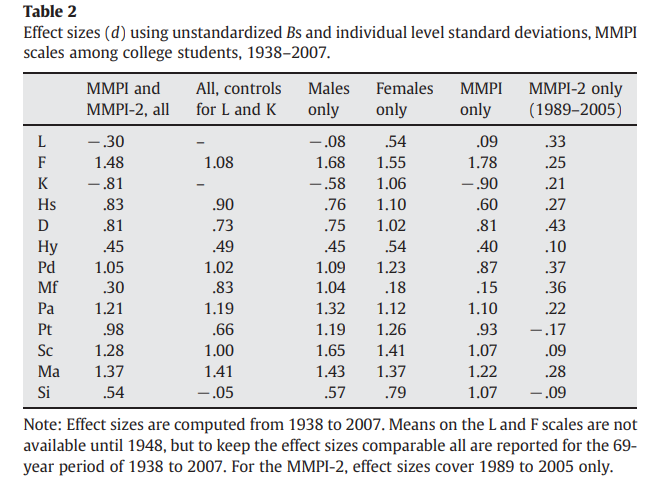
One meta-analysis finds that there has been a large increase in psychopathology within college students between 1938 and 2007 (d = 1.1, p < .001 for the F scale), which does not disappear after controlling for self-presentation using the L and K scale. The F scale measures a proxy for overall psychopathology, the L scale measures the tendency to tell white lies, and the K scale measures the tendency in people to present themselves in a positive or negative light.
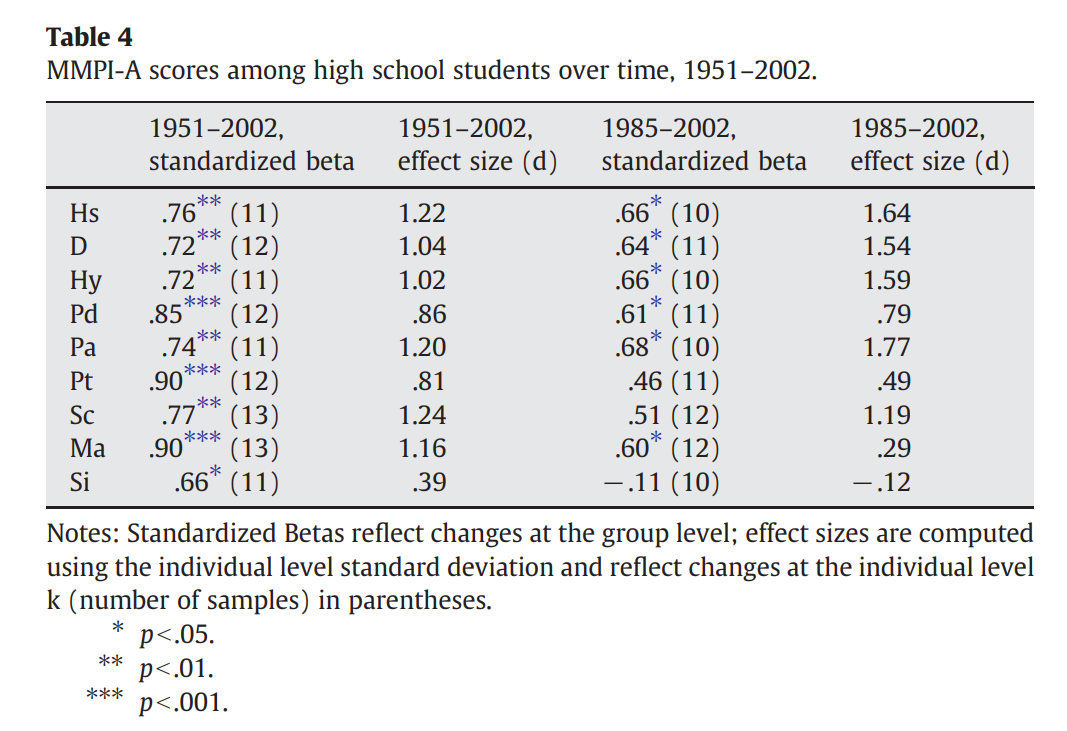
Some, like Steven Pinker, doubt the results of this study because college has become less selective over time. This is probably not the case — these increases are observed within high school students as well, which should not be as strongly affected by the change in selection over time.
Within the period of 1939 to 2007, the average IQ of a college student should have decreased by about 12 points according to the latest meta-analysis. Assuming a correlation of -.35 between psychopathology and IQ, this decrease in selection should have contributed to an increase of .30 SD in psychopathology within college students, far lower than the increase of 1.1 SD that was observed during this period. To posit that this shift is solely due to selection would be to claim that education selects more strongly for mental stability than IQ, which is simply not the case.
How well does this study replicate? So-so. Autism and ADHD diagnosis have become more common, but part of this is due to people with mental retardation being classified as autistic and the floor for diagnosis of these disorders decreasing. Sean Last reviewed the literature on trends in depression and suicidality, and found some weak evidence for an increase in both traits within the youth. A different study on German adolescents who were sampled in 1987 and 2008 evaluated secular trends in psychopathology, and found a statistically significant increase in somatic symptoms, and non-significant increase in internalizing symptoms, and no change in externalizing behaviours. Other studies engaged in obviously non-representative sampling (e.g. people who attempted suicide) or were too low quality to comment on.
All in all, I think the bulk of the evidence does suggest that people are becoming increasingly mentally unstable, but it’s difficult to tell whether that is due to genes or the environment. Although latent personality traits and psychiatric disorders are highly heritable (H^2 = 60-90%), that does not mean that the differences across time are due to heredity — take height for example, a highly heritable (H^2 = 85%) trait that has nonetheless increased by a large amount due to reasons that are not genetic.
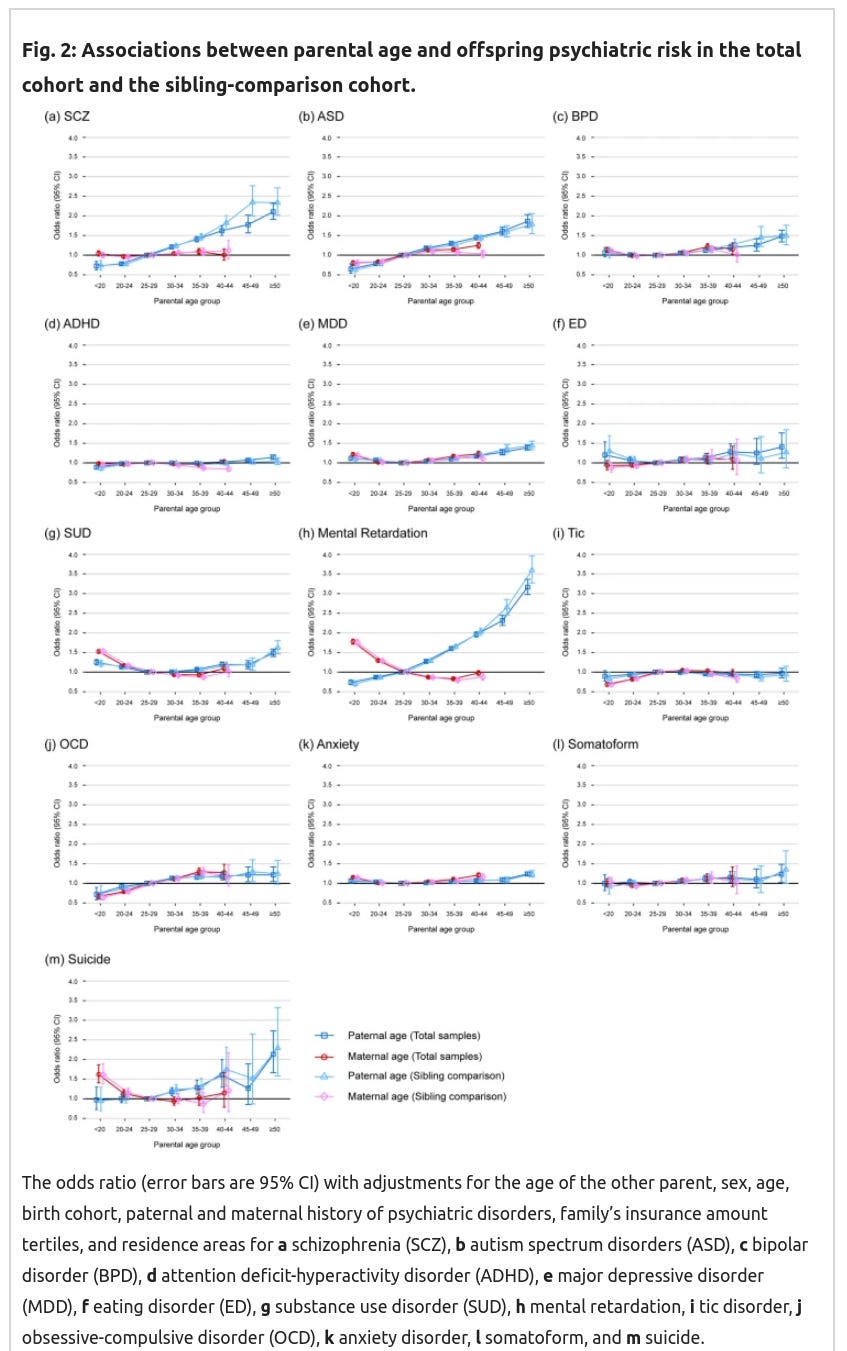
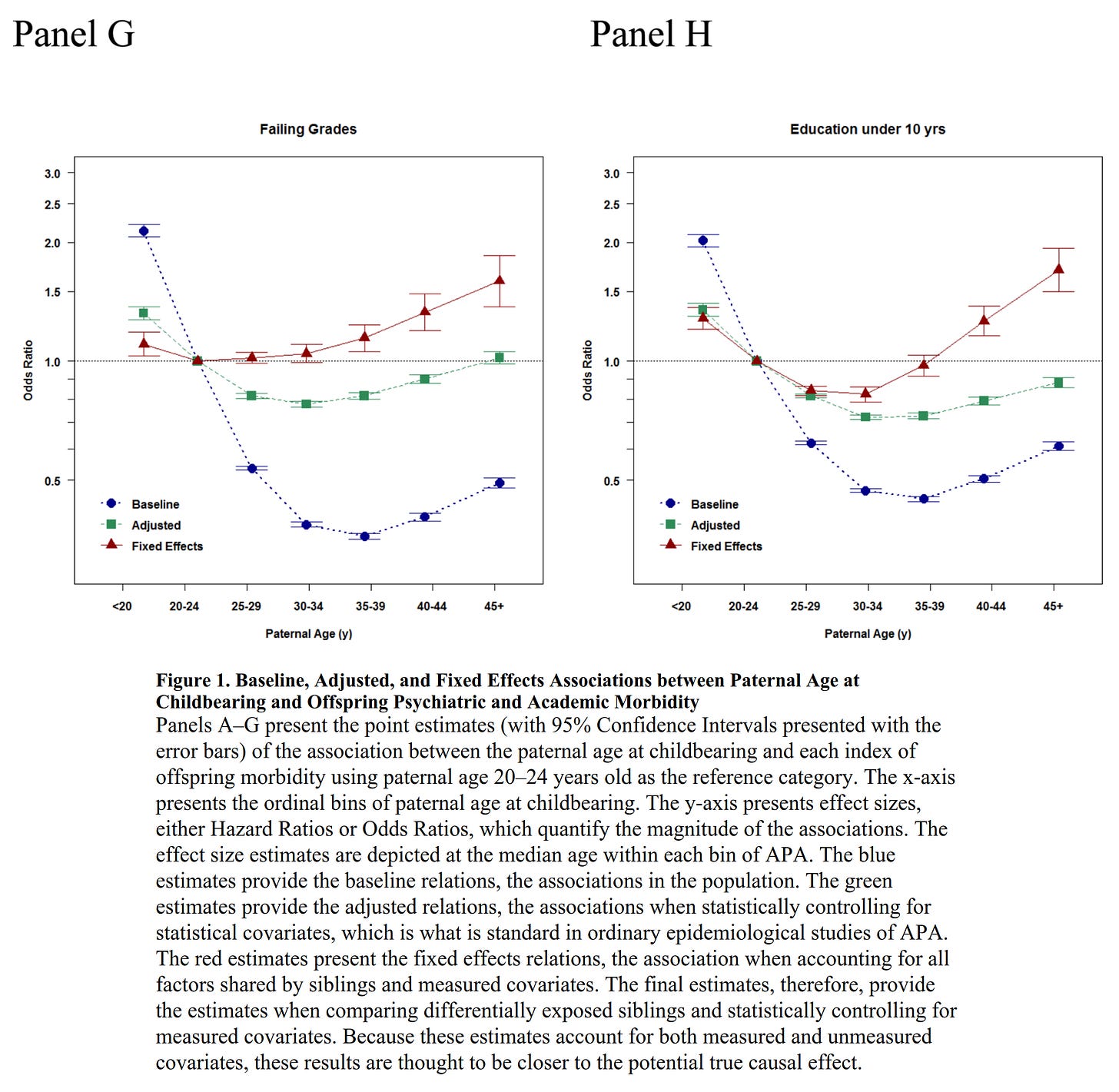
On parental age effects on psychopathology: they probably exist, but there’s a lot of problems with the studies that evaluate the effects — see Emil Kirkegaard’s post on the research:
Conclusion
Let me try to summarize my findings. Here is the evidence that mutational load is not that important:
The French are not uniquely mutationally loaded in comparison to third world populations.
The (admittedly opaque) simulation studies suggest that low purifying selection is not an issue because the mutation rate is much less important than the balance between beneficial and deleterious mutations.
The declines from the negative Flynn effects are way too large to be due to mutational load, and are likely due to non-g variance or immigration.
Controlling for birth order effects attenuates the relationships between parental age and fitness indicators such as intelligence.
Out of the three parental age studies on IQ that exist, all have statistically insignificant negative effects after controlling for birth order.
We have not lost our heads or our money after over a hundred years of industrialization.
There are several plausible purifying selection mechanisms that still exist: abortion, miscarriages, sperm selection, natural selection, and sexual selection.
Here is the evidence that mutational load matters:
(A likely) increase in psychopathology over time in the United States.
Several meta-analyses of reaction time/backwards digit span studies which find declines in performance over time.
The existence of negative Flynn Effects in recent years, though the magnitude of these declines cannot be explained by mutations.
The decline in innovation per capita (which can be explained by many things)
The parental age studies that find psychopathology increases with parental age.
I think there might be something to the changes in psychopathology over time and the parental age effects for it, but the research on these effects is too new to say anything definitive.
What does my intuition say?


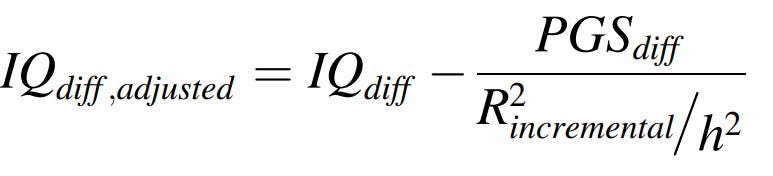
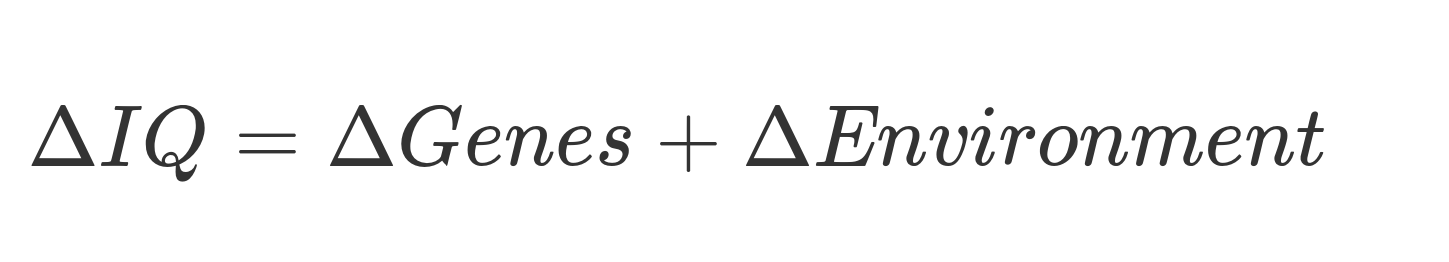

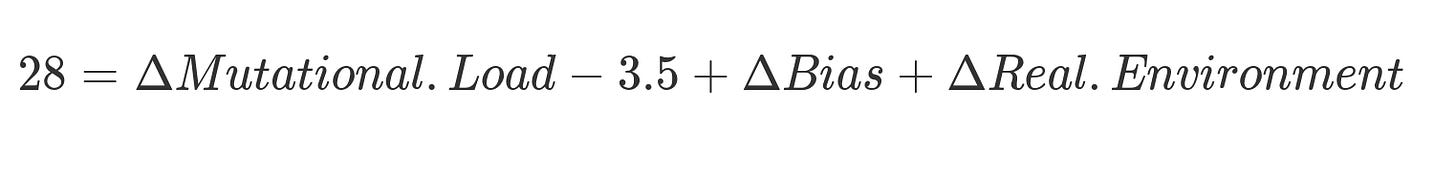
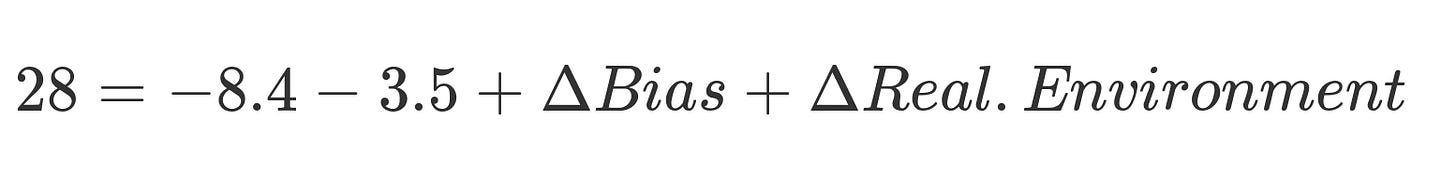
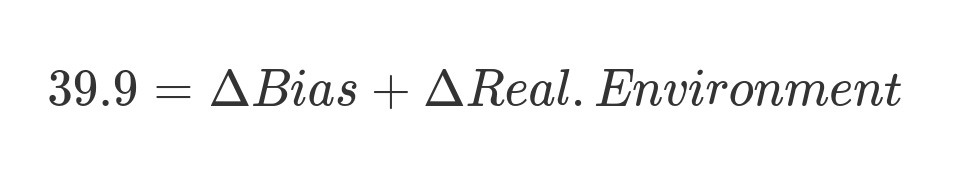








You and Emil Kirkegaard are my favourite social scientists 👨🏿🔬
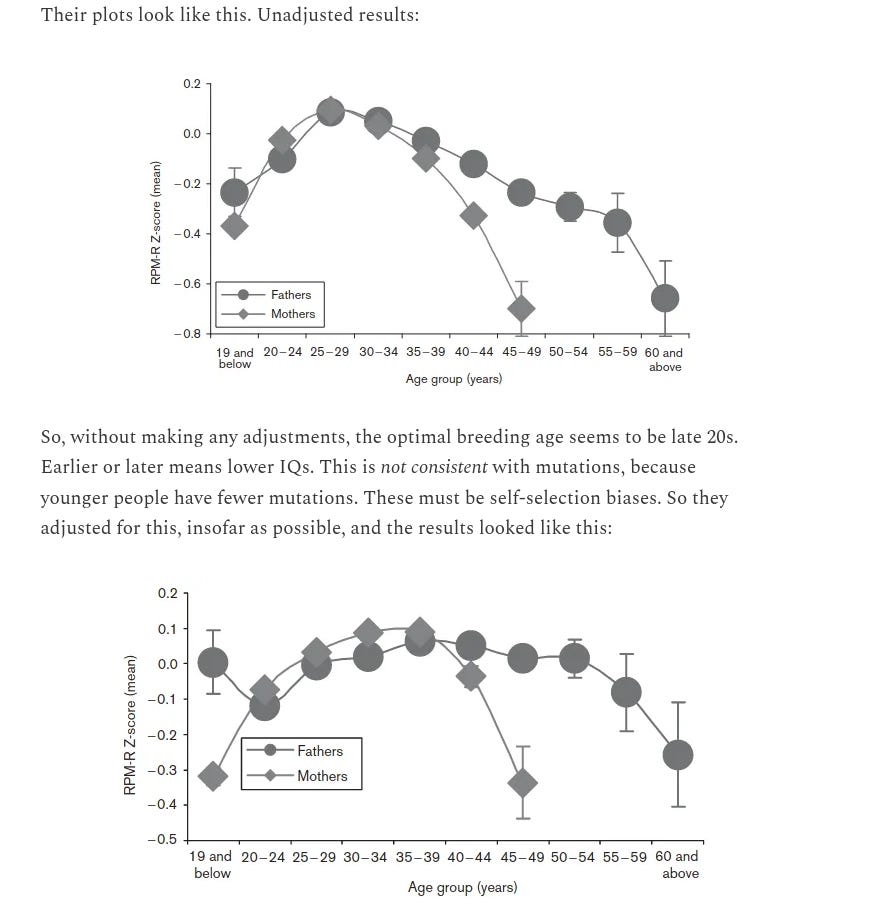
"In addition, the association between paternal age and outcomes such as the number of children between siblings has stayed stagnant in Sweden - whether that was before industrialization occurred or after it occurred. If anything, mutational load appears to have been more of an issue in historical Sweden than modern Sweden."
I really wish people would read this paper more thoroughly. The graph is the sibling control results, which is less appropriate for assessing the relative reproductive success of high-ML vs low-ML than for assessing the causal deleterious effects that ML (Mutational Load) has on phenotypes; this is smaller in modern than historical sweden which is just a cherry on top of the paper's two other findings, these being:
1. for the non-sibling-control results, high-ML parents had a higher absolute number of children in historical sweden than low-ML parents, but in modern sweden, low-ML parents had more children than high-ML parents
2. average paternal age is down; people nowadays start having kids later, but stop having kids earlier, and the latter is slightly more important.
People also seem to not understand the study design here. First of all, there are three generations, let's call grandparent generation g1, parent generation g2, and child generation g3. g1 has children at varying paternal age, and this determines which g2 parents are high/low mutational load, and so it's the relative reproductive outcomes of different g2 individuals that they're studying. Second note, there's a reason that "number of children" appears in the chart twice, and they do not mean the same thing:
"(b) Statistical approach: ...We analysed reproductive success for all offspring, including those who died in childhood or never married."
in other words, when looking at how the ML of g2 individuals affects how many children they have, infant mortality + etc is taken into account unless specified otherwise (i.e. in e4), making m1 the most comprehensive possible estimate of the amount of purifying selection that occurs (and again, m1 finds positive effects of ML on success in historical sweden while finding negative effects in modern sweden).
Another ML null finding:
This k=262 meta-analysis found no correlation between publication year and percent left handed
https://not-equal.org/content/pdf/misc/10.1037.bul0000229.pdf